Урок Решение задач по теме: «Электромагнитные колебания. Колебательный контур»

Урок Решение задач по теме: «Электромагнитные колебания. Колебательный контур»

Задача1. Колебательный контур радиоприёмника настроен на длину волны λ = 2000 м. Индуктивность катушки контура L = 6 мкГн, максимальный ток в ней Imax = 1,6 мА. В контуре используется плоский воздушный конденсатор, расстояние между пластинами которого d = 2 мм. Чему равно максимальное значение напряжённости электрического поля в конденсаторе в процессе колебаний?

Решение.

Согласно закону сохранения энергии

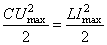(1)

(C – ёмкость конденсатора, Umax — максимальное напряжение на конденсаторе). Формула Томсона для периода электромагнитных колебаний в контуре:

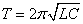. (2)

Формула, связывающая длину волны с периодом колебаний:

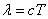
(c – скорость света). Решив систему уравнений (1)-(3), находим величину Umax, откуда получаем для искомой напряжённости поля конденсатора:

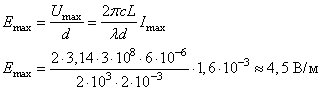
Задача 2. В двух идеальных колебательных контурах с одинаковой индуктивностью происходят свободные электромагнитные колебания, причём период колебаний в первом контуре 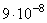с, во втором 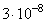с. Во сколько раз амплитудное значение силы тока во втором контуре больше, чем в первом, если максимальный заряд конденсаторов в обоих случаях одинаков?

Решение

Амплитудное значение силы тока в контуре связано с периодом колебаний и максимальным значением заряда конденсатора соотношением

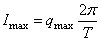.Так как заряды в обоих случаях одинаковы, то отношение максимальных значений токов, дает:

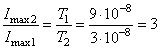,то есть в 3 раза.

Задача 3. На рисунке приведён график зависимости силы тока от времени в колебательном контуре, образованном конденсатором и катушкой, индуктивность которой равна 0,3 Гн. Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.

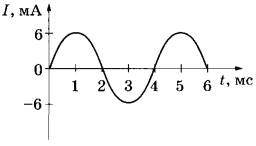
1) Период электромагнитных колебаний равен 4 мс.

2) Максимальное значение энергии электрического поля конденсатора равно 5,4 мкДж.

3) В момент времени 4 мс заряд конденсатора равен нулю.

4) В момент времени 3 мс энергия магнитного поля катушки достигает своего минимума.

5) За первые 6 мс энергия магнитного поля катушки достигла своего максимума 2 раза.

Решение.

1) В колебательном контуре колебание начинается с разрядки конденсатора, что приводит к появлению тока в цепи, затем, возникающая ЭДС в катушке, вновь начинает заряжать конденсатор, но с противоположной полярностью. После этого процесс повторяется, ток начинает течь в обратную сторону и повторная зарядка конденсатора (график тока в отрицательной области) с прежней полярностью завершает колебательный процесс. Таким образом, период колебаний составляет 4 мс.

2) Согласно закону сохранения энергии в колебательном контуре, можно записать, что

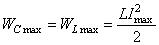Из графика видно, что 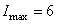мА, тогда

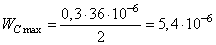Дж

или 5,4 мкДж.

3) Когда ток равен 0 это означает, что конденсатор полностью заряжен.

4) Энергия поля катушки не зависит от знака тока, поэтому при 3 с она достигает своего максимума.

5) В диапазоне 6 с видим три пика тока, следовательно, катушка трижды достигала своего максимума по энергии.

Ответ: 12.

Задача 4. Идеальный колебательный контур состоит из конденсатора и катушки индуктивностью 4 мГн. Заряд на пластинах конденсатора изменяется во времени в соответствии с формулой 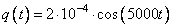(все величины выражены в СИ).

Установите соответствие между физическими величинами и формулами, выражающими их зависимость от времени в условиях данной задачи. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ А) сила тока i(t) в колебательном контуре Б) энергия WL(t) магнитного поля катушки

ФОРМУЛЫ

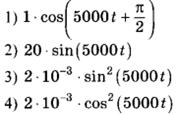
Решение.

А) Сила тока в цепи определяется как 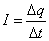, что, в пределе означает производную от q(t) по времени t. Найдем 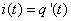, получим:

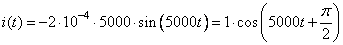Б) Энергия магнитного поля катушки определяется как

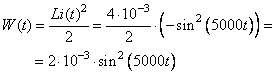
Ответ: 13.

Домашнее задание

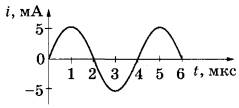
Задача 1. На рисунке приведён график зависимости силы тока i от времени t при свободных гармонических колебаниях в колебательном контуре. Каким станет период свободных колебаний в контуре, если конденсатор в этом контуре заменить на другой конденсатор, ёмкость которого в 4 раза меньше?

Решение.

Из графика видно, что период колебаний тока равен T=4 мкс. Период колебаний колебательного контура определяется выражением 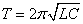, где C – емкость конденсатора; L – индуктивность катушки. Если емкость уменьшить в 4 раза, то период колебаний станет равен:

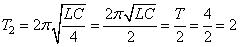мкс.

Задача 2. Если ключ К находится в положении 1, то период собственных электромагнитных колебаний в контуре (см. рисунок) равен 3 мс. Насколько увеличится период собственных электромагнитных колебаний в контуре, если ключ перевести из положения 1 в положение 2?

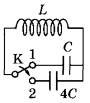
Решение.

Период электромагнитных колебаний определяется по формуле

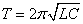При переключении ключа емкость конденсатора становится равной 4C и период становится равным:

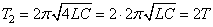то есть увеличивается в 2 раза и составляет 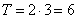мс. В результате период колебаний увеличится на

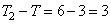мс.