
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Формула Бернулли.
Друзья!
Продолжаем изучать следствия из теорем сложения и умножения
вероятностей:
1. Формула полной вероятности. Формула Байеса.
Пусть событие Аможет произойти только с одним из событий H 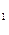 , H
, H 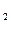 ,…H
,…H 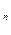
образующих полную группу событий, тогда вероятность события А
вычисляют по формуле полной вероятности:
P(A)=P(H 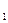 )
)  P
P 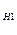 (A)+P(H
(A)+P(H 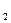 )
)  P
P 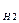 (A)+…+P(H
(A)+…+P(H 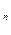 )
) 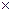 P
P 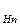 (A)
(A)
Если событие Ауже произошло, то вероятность события H 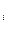 можно переоценить по
можно переоценить по
формуле Байеса:
P 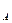 (H
(H 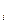 )=
)= 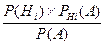 , где i =1,2,…,n, а P(A)- вычисляется по формуле полной
, где i =1,2,…,n, а P(A)- вычисляется по формуле полной
вероятности.
Задача.
- На фабрике, изготовляющей болты, первый автомат производит 25%, второй – 35%, третий – 40% всей продукции. Брак в их продукции составляет соответственно по 5%, 4%, 2%. Найти:
а) вероятность того, что случайно выбранный болт оказался дефектным;
б) вероятность того, что если случайно выбранный болт оказался дефектным, то он произведен первым автоматом.
Решение.
Обозначим через А событие, состоящее в том, что случайно выбранный болт – дефектный.
H 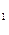 , H
, H 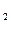 , H
, H 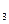 - события, состоящие в том, что этот болт произведен соответственно первым, вторым и третьим автоматом. Очевидно, что H
- события, состоящие в том, что этот болт произведен соответственно первым, вторым и третьим автоматом. Очевидно, что H 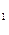 , H
, H 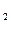 , H
, H 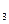 есть полная группа событий. Вероятности этих событий: P(H
есть полная группа событий. Вероятности этих событий: P(H 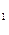 )=0.25, P(H
)=0.25, P(H 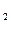 )=0.35, P(H
)=0.35, P(H 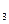 )=0.40
)=0.40
Тогда по формуле полной вероятности:
P(A)=P(H 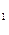 )
) 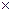 P
P 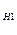 (A)+ P(H
(A)+ P(H 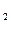 )
) 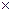 P
P 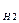 (A)+ P(H
(A)+ P(H 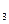 )
) 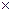 P
P 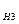 (A)=0.25
(A)=0.25 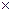 0.05+0.35
0.05+0.35 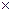 0.04+0.40
0.04+0.40  0.02=0.0345
0.02=0.0345
Теперь требуется определить условную вероятность P 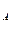 (H
(H 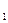 ), т.е. вероятность события H
), т.е. вероятность события H 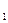 (болт произведен первым автоматом) при условии, что произошло событие А(этот болт оказался дефектным). По формуле Байеса:
(болт произведен первым автоматом) при условии, что произошло событие А(этот болт оказался дефектным). По формуле Байеса:
P 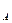 (H
(H 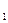 )=
)= 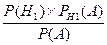 =
= 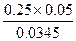 =0.3623
=0.3623
2. В первом ящике 20 деталей, из них 15 стандартных, во втором – 30 деталей, из них 24 стандартных, в третьем – 10 деталей, из них 6 стандартных. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика стандартная.
Решение.
Обозначим события: А –деталь стандартная,
H 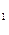 - выбрали первый ящик.
- выбрали первый ящик.
H 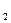 - выбрали второй ящик.
- выбрали второй ящик.
H 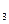 - выбрали третий ящик.
- выбрали третий ящик.
Тогда P(H 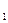 )=
)= 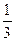 , P(H
, P(H 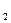 )=
)= 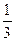 , P(H
, P(H 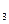 )=
)= 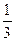 ;
;
Условные вероятности: P 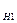 (A)=
(A)= 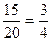 , P
, P  (A)=
(A)= 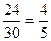 , P
, P  (A)=
(A)= 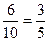 .
.
Вероятность того, что деталь стандартная, вычисляем по формуле:
P(A)=P(H 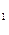 )
) 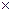 P
P 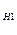 (A)+ P(H
(A)+ P(H 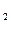 )
) 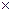 P
P 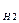 (A)+ P(H
(A)+ P(H 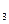 )
)  P
P 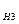 (A)=
(A)= 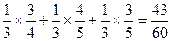
2.Формула Бернулли.
Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют НЕЗАВИСИМЫМИотносительно события А.
Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p, событие наступит ровно k раз (безразлично в какой последовательности), равна
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|