
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Элементы статистики
Элементы статистики
Напомним, что статистика – это наука, которая занимается сбором, обработкой и изучением различных данных, связанных с массовыми явлениями, процессами и событиями.
В статистике исследуют различные совокупности данных – числовых значений случайных величин с учётом частот, с которыми они встречаются в совокупности. При этом совокупность всех данных называют генеральной совокупностью, а любую выбранную из неё часть – выборкой.
Случайными величинами называют такие величины, которые в ходе наблюдений или испытаний могут принимать различные значения. Можно говорить о том, что их значения зависят от случая.
В статистических исследованиях выборку называют репрезентативной, если в ней присутствуют те и только те значения случайной величины, что и в генеральной совокупности, причём частоты имеющихся в ней данных находятся практически в тех же отношениях, что и в генеральной совокупности.
Каждый элемент выборки называют её вариантой. Выборка, полученная в результате наблюдений, бывает неупорядоченной. Упорядочив её, получают вариационный ряд. Разность наибольшего и наименьшего значений случайной величины выборки называется её размахом и обозначается 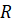 .
.
Совокупность данных иногда бывает полезно охарактеризовать (оценить) одним числом – мерой центральной тенденции числовых значений её элементов. К таким характеристикам относятся мода, медиана и среднее значение.
Мода выборки – это значение случайной величины, имеющее наибольшую частоту в рассматриваемой выборке (обозначается 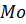 ).
).
Медиана выборки – это число (значение случайной величины), которое «разделяет» соответствующий вариационный ряд на две равные по количеству данных части (обозначается 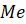 ).
).
Если в упорядоченной выборке нечётное количество данных, то медиана равна серединному из них. Если в упорядоченной выборке чётное количество данных, то медиана равна среднему арифметическому двух серединных чисел.
Среднее значение выборки (или среднее арифметическое) – это число, равное отношению суммы всех чисел выборки к их количеству ( 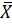 ).
).
Если варианты выборки повторяются, то суммы равных слагаемых можно заменить произведениями.
В статистике часто используют и среднее квадратичное. Если дано 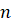 чисел
чисел 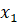 ,
, 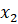 , … ,
, … , 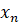 , то их среднее квадратичное
, то их среднее квадратичное 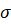 определяется по формуле:
определяется по формуле:
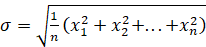 .
.
С помощью среднего квадратичного чаще оценивают совокупности погрешностей или отклонений от нормы.
Если разности между вариантами выборки и её средним значением равны 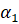 ,
, 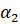 , … ,
, … , 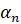 , то среднее арифметическое их квадратов называется дисперсией выборки. Дисперсия равна квадрату среднего квадратичного всех отклонений и вычисляется по формуле:
, то среднее арифметическое их квадратов называется дисперсией выборки. Дисперсия равна квадрату среднего квадратичного всех отклонений и вычисляется по формуле:
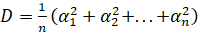 .
.
В математике, в частности в математической статистике, нередко используют также среднее геометрическое и среднее гармоническое, вычисляемые по следующим формулам:
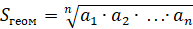 ,
, 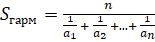 .
.
На практике часто после проведения реальных испытаний составляются таблицы распределения значений случайных величин по частотам (или по относительным частотам), после чего для большей наглядности распределение данных представляют либо в виде диаграммы, либо в виде полигона частот (полигона относительных частот).
Таблица частот, составленная по итогам проведения контрольного среза по математике. В верхней строке указаны оценки, в нижней – количество учеников, получивших ту или иную оценку, другими словами – частота появления этого числа в общем ряду полученных оценок.
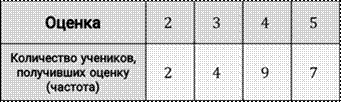
Иногда в таблице для каждого данного указывают не частоту, а отношение частоты к общему числу данных в ряду. Это число, выраженное в процентах, называют относительной частотой, а саму таблицу – таблицей относительных частот.
Таблица относительных частот, составленная по итогам проведения контрольного среза по математике, выглядит следующим образом:
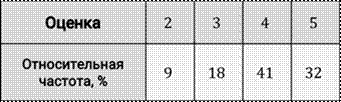
Заметим, что сумма относительных частот составляет 100 %.
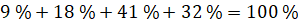
Информацию о той или иной выборке часто подают графически, чаще всего в форме диаграмм.
Столбчатую диаграмму используют тогда, когда хотят проиллюстрировать динамику изменения данных во времени или распределение данных, полученных в результате статистического исследования.
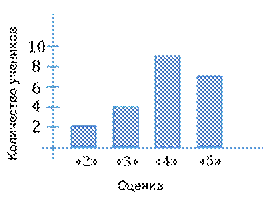
Столбчатую диаграмму из соединённых прямоугольников называют гистограммой.
Иногда вместо гистограммы строят полигон распределения, соединяя отрезками середины верхних оснований последовательных прямоугольников гистограммы.
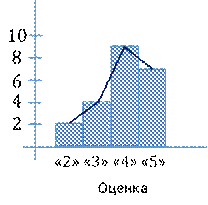
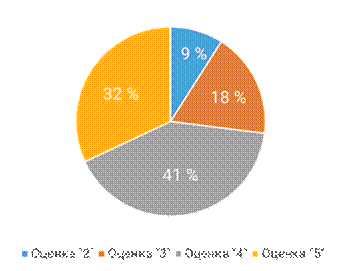
Круговые диаграммы удобно использовать для наглядного изображения соотношения между частями исследуемой совокупности.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задача первая. Выборка включает все натуральные числа меньше 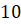 , а кроме того, числа
, а кроме того, числа 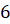 ,
, 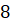 ,
, 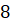 и
и 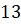 . Постройте её вариационный ряд. Найдите размах выборки, её моду и медиану.
. Постройте её вариационный ряд. Найдите размах выборки, её моду и медиану.
Решение.

Задача вторая. Измерение роста детей младшей группы детского сада представлено следующей выборкой: 92, 96, 95, 96, 94, 97, 98, 94, 95, 96. Найдите размах, моду, медиану и среднее значение этой выборки.
Решение.

Задача третья. Во время медицинского обследования кровяного давления у курсантов (в условиях учебной нагрузки) получены следующие результаты:

Найдите центральные тенденции выборки.
Решение.
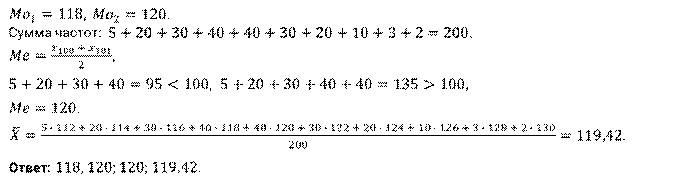
Задача четвёртая. Три фрезеровщика изготовили по 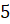 одинаковых деталей длиной
одинаковых деталей длиной 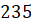 мм, допустив, соответственно, такие погрешности в миллиметрах:
мм, допустив, соответственно, такие погрешности в миллиметрах:
I: 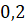 ;
; 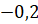 ;
; 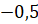 ;
; 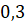 ;
; 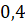 ;
;
II: 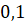 ;
; 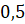 ;
; 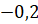 ;
; 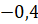 ;
; 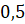 ;
;
III: 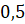 ;
; 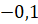 ;
; 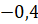 ;
; 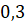 ;
;  .
.
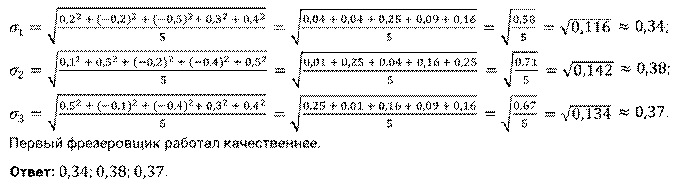
Найдите среднее квадратичное допущенных ими погрешностей. Кто выполнил задание лучше?
Решение.
Задача пятая. Главными составляющими частями воздуха (недалеко от земной поверхности) являются азот – 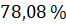 объёма, кислород –
объёма, кислород – 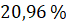 объёма и инертные газы –
объёма и инертные газы – 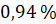 объёма. Количество этих газов в воздухе не изменяется, поэтому их называют постоянными составляющими частями воздуха. Постройте круговую диаграмму состава воздуха. Установите, какой процент объёма занимают другие газы.
объёма. Количество этих газов в воздухе не изменяется, поэтому их называют постоянными составляющими частями воздуха. Постройте круговую диаграмму состава воздуха. Установите, какой процент объёма занимают другие газы.
Решение.
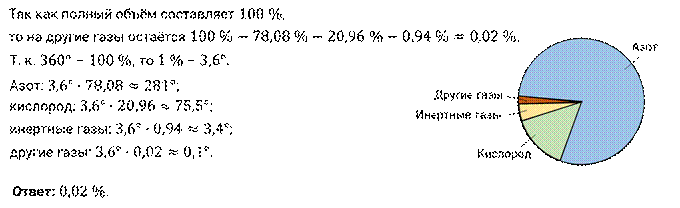
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|