
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тестирование №2-2020 по алгебре.
Тестирование №2-2020 по алгебре.
Вариант 1.
Задача 1. Матрица линейного оператора 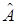 в базисе
в базисе 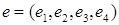 имеет вид
имеет вид

Найти матрицу этого линейного оператора в базисе 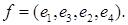
Задача 2.В линейном пространстве 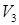 в некотором базисе даны векторы
в некотором базисе даны векторы
 и
и 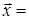
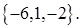
Показать, что векторы 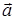 ,
, 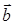 ,
, 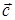 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 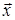 в этом базисе.
в этом базисе.
Задача 3. Как определяется произведение двух линейных операторов?
Используя определение матрицы оператора в данном базисе, доказать, что матрица произведения 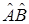 двух линейных операторов равна произведению матриц этих операторов в этом базисе.
двух линейных операторов равна произведению матриц этих операторов в этом базисе.
Вариант 2.
Задача 1. Найдите матрицу оператора дифференцирования 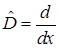 в пространстве
в пространстве 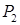 многочленов степени,не превосходящей 2,в базисе
многочленов степени,не превосходящей 2,в базисе 
Задача 2. В линейном пространстве 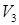 в некотором базисе даны векторы
в некотором базисе даны векторы
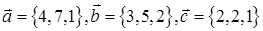 и
и 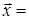
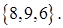
Показать, что векторы 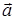 ,
, 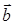 ,
, 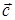 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 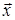 в этом базисе.
в этом базисе.
Задача3.Найдите матрицу перехода от ортонормированного базиса 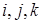 в пространстве
в пространстве 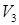 геометрических векторов к базису
геометрических векторов к базису 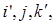 где
где 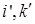 получаются соответственно из векторов
получаются соответственно из векторов
 поворотом их на угол
поворотом их на угол 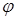 в плоскости этих векторов. Найдите также обратную матрицу.
в плоскости этих векторов. Найдите также обратную матрицу.
Вариант 3.
Задача 1.Элементы  и
и  линейного пространства
линейного пространства 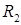 имеют в базисе
имеют в базисе 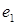 и
и 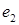 координаты 0,1и1,0. Найти матрицы оператора
координаты 0,1и1,0. Найти матрицы оператора 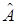 в базисах
в базисах 
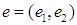 и
и 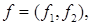 если элементы
если элементы 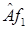 и
и 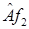 имеют в базисе
имеют в базисе 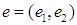 координаты 2,3 и 4,5.
координаты 2,3 и 4,5.
Задача 2. В линейном пространстве 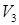 в некотором базисе даны векторы
в некотором базисе даны векторы
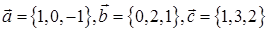 и
и 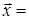

Показать, что векторы 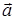 ,
, 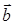 ,
, 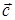 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 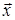 в этом базисе.
в этом базисе.
Задача 3.В базисе 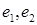 линейного пространства
линейного пространства 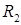 произвольные элементы
произвольные элементы 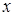 и
и 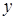 имеют разложения
имеют разложения
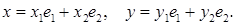
Можно ли в этом пространстве ввести скалярное произведение элементов по формуле
 Ответ обосновать.
Ответ обосновать.
Вариант 4.
Задача 1. Пусть  линейная оболочка функций
линейная оболочка функций  и
и 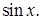 Найдите матрицу обратную к матрице оператора дифференцирования
Найдите матрицу обратную к матрице оператора дифференцирования 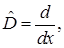 действующего в
действующего в 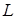 в базисе
в базисе 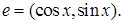
Задача 2. В линейном пространстве 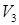 в некотором базисе даны векторы
в некотором базисе даны векторы
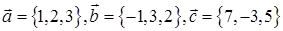 и
и 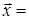
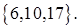
Показать, что векторы 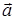 ,
, 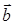 ,
, 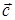 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 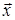 в этом базисе.
в этом базисе.
Задача3. Найдите матрицу перехода от ортонормированного базиса 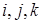 в пространстве
в пространстве 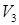 геометрических векторов к базису
геометрических векторов к базису 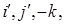 где
где 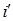 и
и 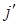 получаются соответственно из векторов
получаются соответственно из векторов
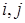 поворотом их на угол
поворотом их на угол 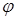 в плоскости этих векторов. Найдите также обратную матрицу.
в плоскости этих векторов. Найдите также обратную матрицу.
Вариант 5.
Задача 1.Произвольный элемент 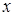 линейного пространства
линейного пространства 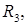 имеющий в базисе
имеющий в базисе 
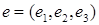 координаты
координаты 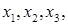 при действии линейного оператора
при действии линейного оператора 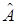 переходит в элемент, имеющий координаты
переходит в элемент, имеющий координаты 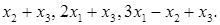 Найдите матрицу оператора
Найдите матрицу оператора 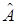 в базисе
в базисе 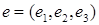
Задача 2. В линейном пространстве 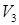 в некотором базисе даны векторы
в некотором базисе даны векторы
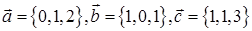 и
и 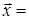
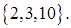
Показать, что векторы 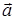 ,
, 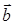 ,
, 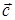 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 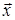 в этом базисе.
в этом базисе.
Задача 3.Найдите матрицу перехода от ортонормированного базиса 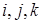 в пространстве
в пространстве 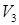 геометрических векторов к базису
геометрических векторов к базису 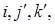 где
где 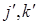 получаются соответственно из векторов
получаются соответственно из векторов
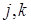 поворотом их на угол
поворотом их на угол 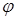 в плоскости этих векторов. Найдите также обратную матрицу.
в плоскости этих векторов. Найдите также обратную матрицу.
Вариант 6.
Задача 1.Матрица линейного оператора 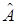 в базисе
в базисе 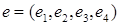 имеет вид
имеет вид 
Найти матрицу этого линейного оператора в базисе 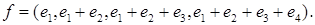
Задача 2. В линейном пространстве 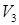 в некотором базисе даны векторы
в некотором базисе даны векторы
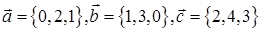 и
и 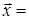
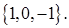
Показать, что векторы 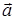 ,
, 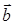 ,
, 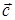 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 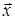 в этом базисе.
в этом базисе.
Задача 3. В базисе 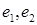 линейного пространства
линейного пространства 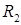 произвольные элементы
произвольные элементы 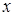 и
и 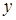 имеют разложения
имеют разложения
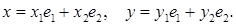
Можно ли в этом пространстве ввести скалярное произведение элементов по формуле
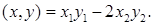 Ответ обосновать.
Ответ обосновать.
Вариант 7.
Задача1.Произвольный элемент 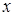 линейного пространства
линейного пространства 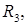 имеющий в базисе
имеющий в базисе 
 координаты
координаты 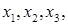 при действии линейного оператора
при действии линейного оператора 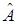 переходит в элемент, имеющий координаты
переходит в элемент, имеющий координаты 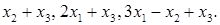 Найдите матрицу оператора
Найдите матрицу оператора  в базисе
в базисе 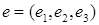
Задача 2. В линейном пространстве 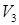 в некотором базисе даны векторы
в некотором базисе даны векторы
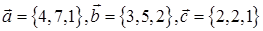 и
и 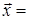
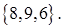
Показать, что векторы  ,
, 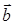 ,
, 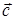 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 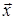 в этом базисе.
в этом базисе.
Задача 3. В базисе  линейного пространства
линейного пространства 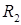 произвольные элементы
произвольные элементы 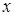 и
и  имеют разложения
имеют разложения
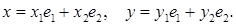
Можно ли в этом пространстве ввести скалярное произведение элементов по формуле
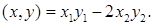 Ответ обосновать.
Ответ обосновать.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|