ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 40. Краткие теоретические сведения. Формулы решений простейших тригонометрических уравнений. Sin x = a Cos x=a

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 40

Тема:Решение тригонометрических уравнений с помощью разложения на множители

Краткие теоретические сведения

Формулы решений простейших тригонометрических уравнений

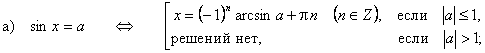
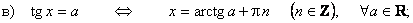
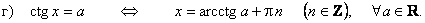
Частные случаи тригонометрических уравнений:

Sin x = a Cos x=a

Если	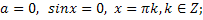Если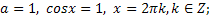
Если	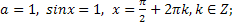Если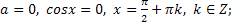
Если	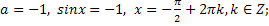Если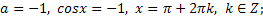

Суть данного метода в том, чтобы путем равносильных преобразований представить левую часть исходного уравнения, содержащую неизвестную величину в какой-либо степени, в виде произведения двух выражений, содержащих неизвестную величину в меньшей степени. При этом справа от знака равенства должен оказаться ноль. Проще всего уяснить эту идею на конкретном примере.

Пример 1. Решите уравнение методом разложения на множители: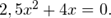

Решение. Осуществим разложение на множители (представим исходное выражение в виде произведения). Для этого вынесем переменную 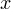за скобки: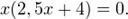

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Следовательно, 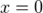или 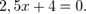Из последнего уравнения получаем: 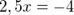или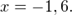

Пример 2. Решите уравнение методом разложения на множители: 2cosx∙cos2x=cosx

Решение. Перенесем все выражения в левую часть и приравняем к нулю:

2cosx∙cos2x-cosx=0

Вынесем общий множитель cosx за скобки:

cosx(2cos2x-1)=0

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю.

cosx = 0 или 2cos2x-1=0

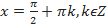cos2x=

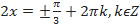(делим всё уравнение на 2)

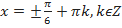
Ответ: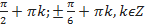

Содержание работы

Вариант 1	Вариант 2

Решите уравнения

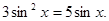2. 2sinx∙sin2x-sinx=0 3. sinx(sinx+1)=0 4. 2 tg²x-tgx=0

1. tgx∙tg2x-2tgx=0 2. cosx(cosx-1)=0 3. ctg²x-3ctgx=0 4. 5 cos²x=2cosx