
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Нахождение первообразной функции
Нахождение первообразной функции
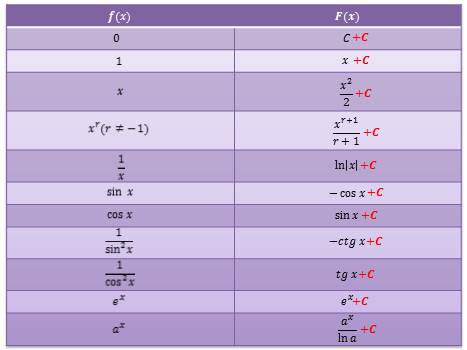
Ещё раз посмотрите что такое первообразная , таблицу первообразных, правила нахождения первообразных
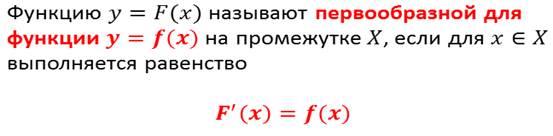
Правила нахождения первообразных .
Пусть F(x) и G(x) – первообразные соответственно функций f(x) и g(x). Тогда:
1. F ( x ) ± G ( x ) – первообразная для f ( x ) ± g ( x );
Первообразная суммы (разности), есть сумма(разность) первообразных
2. k F ( x ) – первообразная для k f ( x ); Постоянный множетель можновыносить за знак первообразной
3. 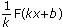 – первообразная для а f ( kx + b ).
– первообразная для а f ( kx + b ).
Пример1. Выяснить, является ли функция F (x) = х 3 – 3х + 1 первообразной для функции f(x) = 3(х 2 – 1).
Решение: Из определения первообразной мы знаемF'(x) =f(x). Значит найдём F'(x) = (х 3 – 3х + 1)′ = 3х 2 – 3 = 3(х 2 – 1) = f(x), т.е. F'(x) = f(x), следовательно, F(x)является первообразной для функции f(x).
Пример2.. Найти все первообразные функции f(x) :
f(x) = х 4 + 3х 2 + 5
Решение: Используя таблицу и правила нахождения первообразных, получим:
Первообразная x4 , будет 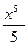 , первообразная 3x2 , будет 3
, первообразная 3x2 , будет 3  первообразная 5 будет 5х. Значит
первообразная 5 будет 5х. Значит
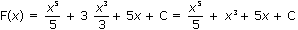
Ответ: 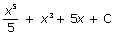
Пример3. . Для функции f(x) = 4 – х 2 найти первообразную, график которой проходит через точку (-3; 10).
Решение:
1) Найдем все первообразные функции f(x): 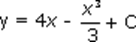
2) Найдем число С , такое, чтобы график функции 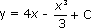 проходил через точку (-3; 10). Подставим х = – 3, y = 10 , получим:
проходил через точку (-3; 10). Подставим х = – 3, y = 10 , получим:
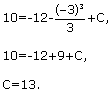
Следовательно, 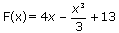 .
.
Ответ: 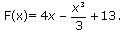
Домашнее задание
1. Является ли функция F(x)=x3+3x-1 первообразной для функции f(x)=3(x3+1)?
2. Для функции f(x)=2x2+3 найдите ту первообразную, график которой проходит через точку (-2;-5)
3. . Какая из данных функций не является первообразной для функции 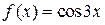 ?
?
1) 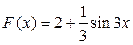 2)
2) 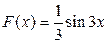 3)
3) 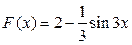 4)
4) 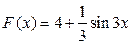
4. Найти первообразную 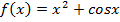
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|