
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
О т в е т ы и у к а з а н и я
13.1 а) Решите уравнение 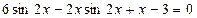 .
.
б) Укажите корни этого уравнения, принадлежащие промежутку 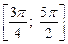 .
.
13.2 а) Решите уравнение 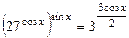 .
.
б) Укажите корни этого уравнения, принадлежащие отрезку 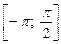 .
.
13.3 а) Решите уравнение 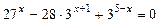 .
.
б) Укажите корни этого уравнения, принадлежащие отрезку 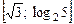 .
.
14.1 В основании пирамиды МАВСТ лежит прямоугольник АВСТ со стороной АВ = 5 и диагональю ВТ = 9. Все боковые рёбра пирамиды равны 5. На диагонали ВТ основания АВСТ отмечена точка Е , а на ребре АМ – точка Р так, что МР = ВЕ = 4.
а) Докажите, что плоскость СЕР параллельна ребру МВ.
б) Плоскость СЕР пересекает ребро МТ в точке К. Найдите расстояние
от точки К до плоскости АВС.
14.2 В основании прямой треугольной призмы ABCA1B1C1 лежит равнобедренный (AB = BC) треугольник ABC . Точка K – середина A1B1 , а точка M делит ребро AC в отношении AM : MC = 1 : 3 .
а) Докажите, что KM перпендикулярно AC .
б) Найдите угол между прямой KM и плоскостью ABB1 , если AB = 6 ,
AC = 8 и AA1 = 3 .
15 Решите неравенство 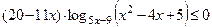 .
.
16 Диагонали равнобедренной трапеции ABCD с основаниями BC и AD перпендикулярны. Окружность с диаметром AD пересекает боковую сторону CD в точке M , а окружность с диаметром CD пересекает основание AD в точке N . Отрезки AM и CN пересекаются в точке P .
а) Докажите, что в четырёхугольник ABCP можно вписать окружность.
б) Найдите радиус этой окружности, если BC = 7, AD = 23 .
18.1 Найдите все значения a , при каждом из которых уравнение  имеет ровно три различных корня.
имеет ровно три различных корня.
18.2 Найдите все значения параметра а , при каждом из которых уравнение 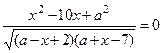 имеет ровно одно решение на отрезке [5; 8] .
имеет ровно одно решение на отрезке [5; 8] .
19.1 На доске написано 30 различных натуральных чисел, десятичная запись которых оканчивается или на цифру 2 , или на цифру 6 . Сумма записанных чисел равна 2454 .
а) Может ли на доске быть поровну чисел, оканчивающихся на 2 и на 6 ?
б) Может ли ровно одно число на доске оканчиваться на 6 ?
в) Какое наименьшее количество чисел, оканчивающихся на 6 ,
может быть записано на доске?
19.2 Каждый из 28 студентов или писал одну из двух контрольных работ, или писал обе контрольные работы. За каждую работу можно было получить целое число баллов от 0 до 20 включительно. По каждой из двух контрольных работ в отдельности средний балл составил 15 . Затем каждый студент назвал наибольший из своих баллов (если студент писал одну работу, то он назвал балл за неё). Среднее арифметическое названных баллов равно А .
а) Приведите пример, когда А меньше 15.
б) Могло ли значение А быть равным 5?
в) Какое наименьшее значение могло принимать А , если обе контрольные
работы писали ровно 10 студентов?
О т в е т ы и у к а з а н и я
13.1 а) 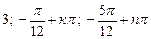 . б)
. б)  .
.
13.2 а) 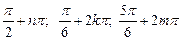 б)
б) 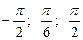
13.3 а) 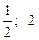 б)
б) 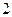 .
.
14.1 б) 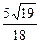 .
.
14.2 б) 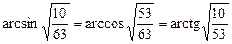 .
.
15 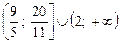 .
.
16 а) Покажите, что ВС = СР и АВ = АР . б) 4,375 .
18.1 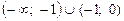 .
.
18.2 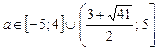 .
.
19.1 Если n чисел оканчиваются на 6 , а (30 – n) чисел оканчиваются на 2 , то сумма всех чисел оканчивается на ту же цифру, что и 6n + 2(30 – n) = 60 + 4n, то есть на ту же цифру, что и 4n . Поэтому n = 1 + 5k . Далее, сумма все тридцати чисел не меньше, чем 6 + 16 + … + 6 + 10(n – 1) + 2 + 12 + … + 2 + 10(29 – n) = 10n2 – 296n + 4410 . Поэтому 10n2 – 296n + 4410 не больше, чем 2454 и, следовательно, n = 11 или n = 16 .
а) нет, так как n не может быть равно 15;
б) нет, так как n не может быть равно 29;
в) 11 или 16 .
Пример для n = 11: 6 + 16 + … + 96 + 196 + 2 + 12 + … + 182 = 2454 .
Пример для n = 16: 6 + 16 + … + 146 + 376 + 2 + 12 + … + 132 = 2454 .
19.2 а) да, например: 20 студентов написали обе контрольные на 20 баллов и по 4 человека написали только 1-ю и только 2-ю контрольные на 10 баллов;
б) нет; в) 95/7.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|