Преподаватель - Брыкало А.А.. Конспект урока «Математика». Ход урока

Преподаватель - Брыкало А.А.

brukalo_aa@mail.ru

https://vk.com/id399759339

Конспект урока «Математика»

Дата01.06.2020

Группа87профессия«Машинист крана (крановщик)» курс2

Тема 123: «Преобразование выражений, содержащих радикалы»

Форма работы:индивидуальная, электронное обучение

Тип урока:урок обобщения и повторения материала

Продолжительность урока: 1 час

Цель урока:повторить материал по теме «Преобразование выражений, содержащих радикалы»

Используемая литература:

Учебник: Математика. Алгебра и начала математического анализа. 10-11 классы: учебник для общеобразовательных организаций: базовый и углубленные уровни./Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.- 5 изд.- М.: Просвещение, 2018г

Интернет-ресурсы:

Методика преподавания математики http://methmath.chat.ru/

Ход урока

Организационный этап:

Мотивационный модуль

Тема сегодняшнего урока «Преобразование выражений, содержащих радикалы».

Основная часть:

Объясняющий модуль

Теоретический материал для самостоятельного изучения

1. Повторите теоретический материал.

1. Определение.

Корнем n-й степени из неотрицательного числа а называется такое неотрицательное число b, которое при возведении в степень n дает число а.

Приведем математическую запись определения:

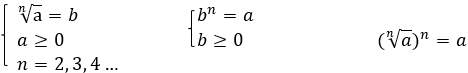
Например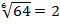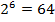: , т. к. ; , т. к. ,

Напомним, что арифметическим корнем называется неотрицательный корень. В нашем случае 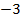– отрицательное число, но – положительное, таким образом, – это арифметический корень.

Вспомним основные свойства арифметических корней:

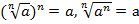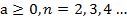
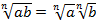при

, при 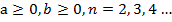(теорема 1);

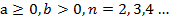, при (теорема 2);

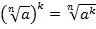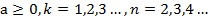, при (теорема 3);

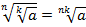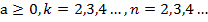, при (теорема 4);

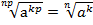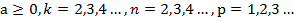при (теорема 5);

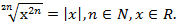
2. Упрощение выражений, примеры

При решении задач мы пользуемся определением и свойствами корня n-й степени.

Пример 1

В результате преобразования получили выражение:

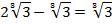
Пример 2

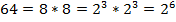
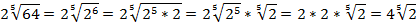
Разложим составное число 486 на простые множители:

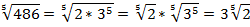
В результате преобразований получаем:

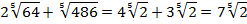
Пример 3

Очевидно, что для решения данного задания необходимо применить формулу сокращенного умножения, а именно: 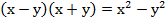– формула разности квадратов.

В нашем случае 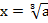, , 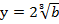получаем:

3. Сокращение дробей, примеры

Одной из типовых задач является задача на сокращение дробей.

Пример 4

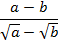
Отметим некоторые ограничения. Для того чтобы существовали заданные корни, необходимо выполнение условий: 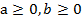. Для того чтобы существовала дробь: .

Преобразуем числитель дроби:

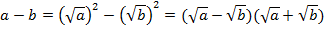
Таким образом, заданную дробь можно записать в следующем виде:

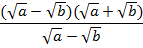
Поскольку мы заранее оговорили, что знаменатель не равен нулю, т. е. , имеем право сократить дробь:

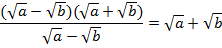
Пример 5:

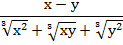
В данном случае также нужно воспользоваться формулой сокращенного умножения.

Таким образом, заданную дробь можно записать в следующем виде:

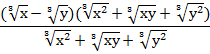
Чтобы иметь право сократить дробь, оговорим, что знаменатель ее не должен быть равен нулю, для этого х и у не должны одновременно быть равны нулю, тогда получаем ответ:

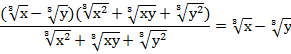
Домашнее задание:

Составьте опорный конспект