Раздел 13. Итоговое повторение курса математики

03.06.20 г.

Раздел 13. Итоговое повторение курса математики

Тема 13.12. Производная. Понятие о производной функции, её геометрический и физический смысл

Производная

Производной функции y = f (x) в точке x₀называется предел:

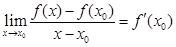
Если этот предел существует, то функция f (x) называется дифференцируемой в точке x₀:

Производная функции: у(x) обозначается так:

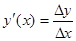
Вычисление производной на основе определения:

1) найти разность: у(x)-у(x₀);

2) найти отношение: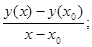

3) найти предел этого отношения, при х→х₀.

Геометрический смысл производной

Рассмотрим график функции: y = f (x):

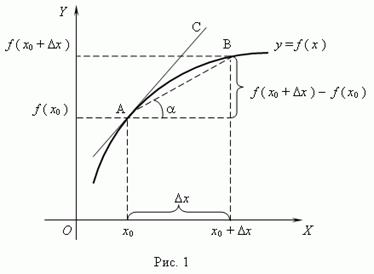
Из рис. 1 видно, что для любых двух точек A и B графика функции:

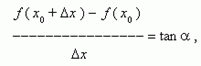
где - угол наклона секущей AB.

Производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.В этом и состоит геометрический смыслпроизводной.

Уравнение касательной

y = f (x₀) + f ’(x₀) · (x – x₀) .

Механический смысл производной

Скорость – это производная координаты по времени.В этом и состоит механический смысл производной. Аналогично, ускорение – это производная скорости по времени:

a = v’ (t).

Производные суммы, разности, произведения, частного

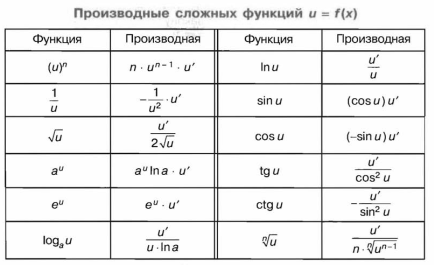
Производные основных элементарных функций

Более подробно можно посмотреть: Богомолов, Н.В.Математика: учебник для СПО / Н.В. Богомолов, П.И. Самойленко. — 5-е изд., перераб. и доп. — М.: Изд-во Юрайт, 2019. — 401 с. — (Серия: Профессиональное образование). — ISBN 978-5-534-07878-7. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://www.biblio-online.ru/bcode/433286.