Конспект урока Законы движения планет Солнечной системы

Конспект урока "Законы движения планет Солнечной системы"

Вы уже знаете, что революционная идея Николая Коперника о гелиоцентрической системе мироустройства дала невероятный толчок развитию астрономии. Однако, если вы помните, Коперник в своём учении не отказался от мыслей Аристотеля о "совершенстве" орбит планет. Поэтому для объяснения многих явлений (например, попятного движения планет), в его теории всё ещё присутствовали эпициклы и деференты.

При этом многие учёные считали, что движение небесных тел должно быть равномерным и по «самой совершенной кривой», то есть окружности. Поэтому до конца XVI века им не удавалось точно рассчитать относительное положение планет на несколько лет вперёд. Теория давала заметное расхождение с результатами наблюдений.

Лишь в начале XVII века австрийский астроном Иоганн Кеплер открыл кинематические законы движения планет. В своих поисках он исходил из убеждения, что «в мире правит число», высказанного ещё Пифагором. Кеплер пытался сопоставить характеристики движения планет с закономерностями музыкальной гаммы, длиной сторон, описанных и вписанных в орбиты планет многоугольников и так далее.

Но увы, каждый раз сравнив свою модель с наблюдаемыми орбитами планет, Кеплер вынужден был признавать, что их реальное поведение не вписывается в очерченные им стройные рамки. По меткому замечанию современного британского биолога Джона Холдейна, «идея Вселенной как геометрически совершенного произведения искусства оказалась ещё одной прекрасной гипотезой, разрушенной уродливыми фактами».

Лишь переехав в Прагу и став учеником датского астронома Тихо Браге, Кеплер натолкнулся на идеи, по-настоящему обессмертившие его имя в анналах науки.

Представим себе проблему, с которой столкнулся Кеплер, следующим образом. Мы находимся на планете, которая, во-первых, вращается вокруг своей оси, а во-вторых, обращается вокруг Солнца по неизвестной нам орбите. Глядя в небо, мы видим другие планеты, которые также движутся по неизвестным нам орбитам. Вопрос: как по данным наблюдений, сделанных на одном вращающемся вокруг оси и вокруг Солнца шарике, определить орбиту и скорость движения других планет?

Кажется, что вопрос достаточно сложный, даже при современном уровне компьютеров. А у Кеплера их не было и, тем не менее, ему удалось найти ответ!

Наблюдая за движением Марса в пространстве, а также воспользовавшись многолетними определениями координат и конфигураций этой планеты, проведёнными Тихо Браге, Кеплер обратил внимание на то, что Марс движется неравномерно. Он решил построить орбиту Марса. Для этого он сделал небольшое приближение, посчитав орбиту Земли круговой (что не противоречило наблюдениям). Затем он рассуждал примерно так. Пусть нам известно угловое расстояние Марса (точка М на рисунке) от точки весеннего равноденствия во время одного из противостояний планеты, то есть его прямое восхождение α₁.

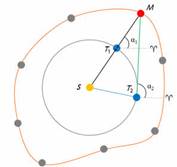
Т₁ — это положение Земли во время противостояния с Марсом.

Для того, чтобы Марс оказался вновь в этой же точке своей орбиты, должно пройти 687 суток (таков звёздный период обращения Марса). Сидерический же период Земли равен 365 суткам. Поэтому, она не успеет «добежать» до точки T₁ и в этот момент будет находиться на своей орбите в точке Т₂. Следовательно, для наблюдателя измениться прямое восхождение Марса. Так вот раз за разом изучая различные противостояния Марса Кеплер получил целый ряд точек. Соединив их плавной кривой, он построил орбиту этой планеты, которая, как оказалось, не являлась окружностью.

Теперь Кеплер был поставлен перед необходимостью сделать выбор одного из двух возможных решений: считать, что орбита Марса представляет собой окружность, и допустить, что на некоторых участках орбиты вычисленные координаты планеты расходятся с наблюдениями; или же считать, что все наблюдения были правильными, а орбита планеты действительно не является окружностью. Будучи уверенным в точности своих наблюдений и наблюдений Тихо Браге, Кеплер выбрал второе решение и установил, что наилучшим образом положения Марса на орбите совпадают с кривой, которая называется эллипсом. При этом Солнце располагается не в его центре. В результате им был сформулирован закон, который впоследствии назвали первым законом Кеплера: все планеты обращаются по эллипсам, в одном из фокусов которых находится Солнце.

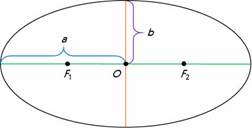На рисунке точка О — это центр эллипса, а F₁ и F₂ — его фокусы.

Проходящий через фокусы эллипса отрезок, концы которого лежат на эллипсе, называется его большой осью.

А отрезок, проходящий через центр эллипса перпендикулярно большой оси, называетсямалой осью эллипса.

Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях, называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются малыми буквами a и b.

Отличие эллипса от окружности характеризуется величиной его эксцентриситета. Он равен половине отношения фокусного расстояния эллипса к его большой полуоси:

Отметим, что в случае, когда эксцентриситет эллипса равен нулю, фокусы и центр эллипса сливаются в одну точку — эллипс превращается в окружность.

Теперь предположим, что Солнце расположено в фокусе F₁. Тогда ближайшая к Солнцу точка орбиты планеты называется перигелием. А наиболее удалённая от Солнца точка, называется афелием.

Например, у земной орбиты эксцентриситет равен 0,017, то есть орбита действительно почти круговая. В перигелии наша планета находится в начале января. Расстояние до Солнца составляет около 147 миллионов километров. Афелий Земля проходит в начале июля, а афелийное расстояние составляет чуть более 152 миллионов километров.

Но вернёмся к Кеплеру и построенной им траектории Марса. Изучив расположения полученных точек, он увидел, что скорость Марса по орбите меняется. Но при этом радиус-вектор планеты (то есть линия, соединяющая центр Солнца с центром планеты) за равные промежутки времени описывает равновеликие площади.

Обнаруженная закономерность впоследствии получила название второго закона Кеплера (иногда его называют законом площадей).

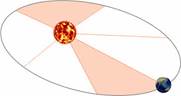
Чтобы лучше понять его физический смысл, вспомните своё детство. Наверняка, вам доводилось на детской площадке раскручиваться вокруг столба, ухватившись за него руками. Фактически, планеты обращаются вокруг Солнца аналогичным образом. Чем дальше от Солнца уводит планету эллиптическая орбита, тем медленнее движение, чем ближе к Солнцу — тем быстрее движется планета.

Объяснить данный закон можно на основе закона сохранения энергии. Из физики вам известно, что полная механическая энергия замкнутой системы тел, между которыми действуют силы тяготения, остаётся неизменной при любых движениях тел этой системы. Поэтому сумма кинетической и потенциальной энергий планеты, которая движется вокруг Солнца, неизменна в каждой точке орбиты планеты. Приближаясь к Солнцу потенциальная энергия планеты уменьшается, в следствии уменьшения расстояния до Солнца. Поэтому её кинетическая энергия должна увеличиваться. А сделать это можно лишь за счёт увеличения скорости.

Таким образом, скорость движения планеты по орбите меняется, принимая максимальное значение в перигелии и минимальное в афелии.

Первый и второй законы были опубликованы Кеплером в 1609 году в книге «Новая астрономия, или Физика небес, изложенная в исследованиях движения планеты Марс...». Хотя реально первый закон Кеплера был открыт в тысяча шестьсот пятом 1605 году, а второй — тысяча шестьсот втором 1602.

Свой третий закон Кеплер сформулировал лишь в 1618 году. Он гласит, что квадраты сидерических периодов обращения двух планет относятся как кубы больших полуосей их орбит:

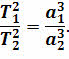Вот что писал по этому поводу сам Кеплер: «То, что 16 лет тому назад я решил искать, ... наконец найдено, и это открытие превзошло все мои самые смелые ожидания...».

И действительно, третий закон заслуживает самой высокой оценки. Ведь он позволяет вычислить относительные расстояния планет от Солнца, используя уже известные их периоды обращения вокруг него. При этом не нужно вычислять расстояния от Солнца до каждой планеты, достаточно измерить это расстояние для одной из них, например, Земли. Кстати, для простоты вычислений, величину большой полуоси́ орбиты Земли приняли равной одной астрономической единице (1 а. е.). Эта единица измерения стала основой для вычисления всех остальных расстояний в Солнечной системе.

Ещё раз обратим ваше внимание на то, что Кеплер открыл свои законы исходя только из собственных наблюдений, и наблюдений Тихо Браге. Если бы вы спросили его, чем обусловлена эллиптичность орбит или равенство площадей секторов, он бы вам не ответил. Это просто следовало из проведённого им анализа. Если бы вы спросили его об орбитальном движении планет в других звёздных системах, он также не нашёл бы ответа на этот вопрос.

Однако гений Кеплера в том и заключался, что он смог увидеть то, во что остальные отказывались верить. А строгое математическое доказательство его законы получили лишь после того, как Ньютоном были открыты закон Всемирного тяготения и закон сохранения момента импульса (известный нам второй закон Ньютона). Но об этом в следующий раз. А сейчас давайте решим с вами одну небольшую задачку. Определите период обращения астероида Россия, если большая полуось его орбиты равна 2,55 а. е.