- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Контрольная работа «Площади поверхностей геометрических тел»
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 1.
| 1. | 
|
| 2. | Прямоугольник, диагональ которого равна 18 см и наклонена к основанию под углом 300, является осевым сечением цилиндра. Найдите площадь полной поверхности цилиндра. |
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 2.
| 1. | Стороны основания прямоугольного параллелепипеда равны 6 и 8 см, а площадь диагонального сечения 180 см2. Вычислите площадь полной поверхности параллелепипеда. |
| 2. | Высота конуса 6 дм, образующая 10 дм. Найдите площадь боковой поверхности конуса. |
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 3.
| 1. | Сторона правильной треугольной пирамиды равна 6 см, а высота 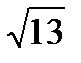 см. Найдите площадь боковой поверхности пирамиды.
|
| 2. | Образующая усеченного конуса равна l и наклонена к плоскости основания под углом 600, а отношение площадей его оснований равно 4. Вычислить площадь полной поверхности этого усеченного конуса. |
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 4.
| 1. |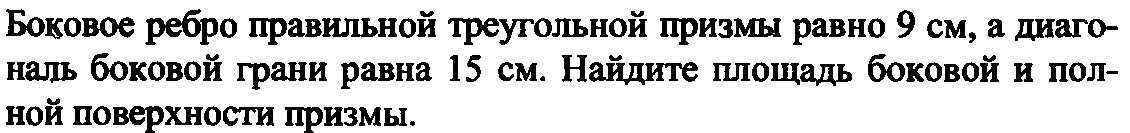 
|
| 2. | Стороны прямоугольника 4 см и 5 см. Найдите площадь полной поверхности тела, полученного при вращении прямоугольника вокруг его меньшей стороны. |
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 5.
| 1. | В прямом параллелепипеде стороны основания равны 3 и 8 см, и образуют угол 600. Большая диагональ параллелепипеда равна 49 см. Вычислите площадь боковой поверхности параллелепипеда. |
| 2. |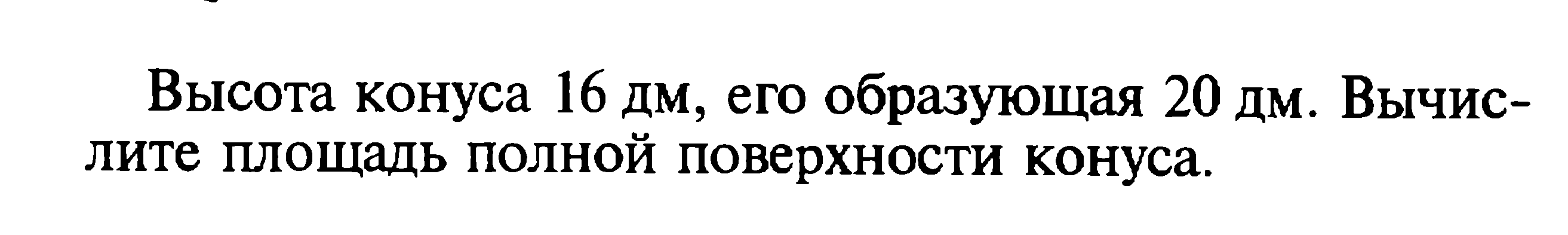 
|
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 6.
| 1. | Боковое ребро правильной треугольной пирамиды равно 5 см, а высота 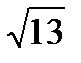см. Найдите площадь боковой поверхности пирамиды.
|
| 2. | Высота усеченного конуса 6 см, радиусы его оснований 10 см и 2 см. Вычислите а) площадь боковой поверхности усеченного конуса; б) полной поверхности усеченного конуса. |
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 7.
| 1. | Основанием прямой призмы ABCDA1B1C1D1 является параллелограмм ABCD со сторонами 6 см и 12 см и углом 60°. Диагональ B1D призмы образует с плоскостью основания угол в 30°. Найдите площадь полной поверхности призмы. |
| 2. |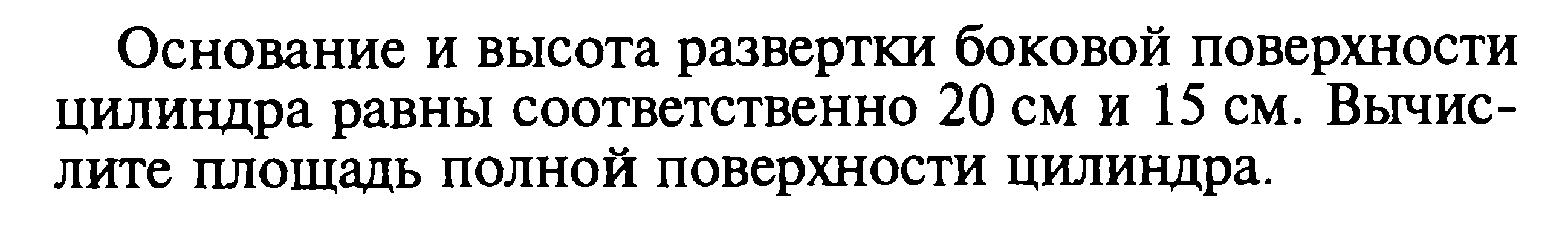 
|
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 8.
| 1. | В прямом параллелепипеде длины сторон основания равны 6 м и 8 м, причем эти стороны образуют угол 300, длина бокового ребра 5 м. Найдите Sполн этого параллелепипеда. |
| 2. | 
|
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 9.
| 1. | Стороны оснований правильной усеченной треугольной пирамиды равны 6 см и 4 см, а боковое ребро — 8 см. Найти площадь полной поверхности усеченной пирамиды. |
| 2. | Длина образующей конуса 24 см. Углом между образующей и плоскостью основания 600. Вычислите площадь боковой поверхности конуса. |
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 10.
| 1. | Основанием прямой призмы ABCDA1B1C1D1 является параллелограмм ABCD со сторонами 4 см и 4 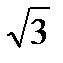 см и углом 30°. Диагональ AC1 призмы образует с плоскостью основания угол в 60°. Найдите площадь полной поверхности призмы.
|
| 2. | 
|
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 11.
| 1. | В правильной четырехугольной усеченной пирамиде длины сторон оснований равны 8 м и 2 м, высота - 4 м. Найдите Sполн. |
| 2. | Прямоугольный треугольник с катетами 6 см и 8 см вращается вокруг меньшего катета. Вычислите площади боковой и полной поверхностей образованного при этом вращении конуса. |
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 12.
| 1. | Основанием прямой призмы ABCDA1B1C1D1 является параллелограмм ABCD со сторонами 6 см и 6 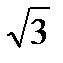см и углом 150°. Диагональ B1D призмы образует с плоскостью основания угол в 60°.Найдите площадь полной поверхности призмы.
|
| 2. | Радиусы оснований усеченного конуса 2 дм и 5 дм, высота 4 дм. Найти Sбок. п. |
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 13.
| 1. | Основанием прямого параллелепипеда служит ромб, длины диагоналей которого 6 см и 8 см, длина диагонали боковой грани равна 13 см. Найдите Sполн параллелепипеда. |
| 2. | 
|
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 14.
| 1. | Основание пирамиды – правильный треугольник со стороной 10 см. Одно из боковых ребер перпендикулярно плоскости основания и равно 5 см. Вычислить площадь боковой поверхности. |
| 2. | 
|
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 15
| 1. | Основанием прямой призмы ABCDA1B1C1D1 является параллелограмм ABCD со сторонами 6 см и 12 см и углом 60°. Диагональ B1D призмы образует с плоскостью основания угол в 30°. Найдите площадь полной поверхности призмы. |
| 2. | Диаметры оснований усеченного конуса 10 см и 16 см, высота 4 см. Найти площадь полной поверхности Sп. п. |
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 16.
| 1. | Найдите площадь полной поверхности прямого параллелепипеда, стороны основания которого равны 8 мм и 12 мм и образуют угол 300, а боковое ребро равно 10 мм. |
| 2. | 
|
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 17.
| 1. | Стороны оснований правильной усеченной треугольной пирамиды равны 6 см и 12 см, а высота 1 см. Вычислите Sбок. |
| 2. | 
|
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 18.
| 1. | 
|
| 2. | Длина образующей конуса 24 см. Углом между образующей и плоскостью основания 600. Вычислите площадь боковой поверхности конуса. |
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 19.
| 1. | Основанием прямого параллелепипеда служит ромб, длины диагоналей которого 6 см и 8 см, длина диагонали боковой грани равна 13 см. Найдите Sполн параллелепипеда. |
| 2. | Образующая усеченного конуса равна l и наклонена к плоскости основания под углом 600, а отношение площадей его оснований равно 4. Вычислить площадь полной поверхности этого усеченного конуса. |
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 20.
| 1. | В правильной четырехугольной усеченной пирамиде длины сторон оснований равны 8 м и 2 м, высота - 4 м. Найдите Sполн. |
| 2. | Диаметры оснований усеченного конуса 10 см и 16 см, высота 4 см. Найти площадь полной поверхности Sп. п. |
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 21.
| 1. |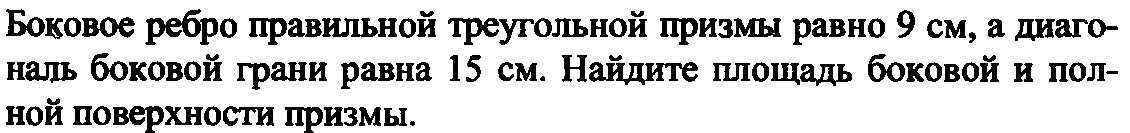
|
| 2. | 
|
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 22.
| 1. | Стороны оснований правильной усеченной треугольной пирамиды равны 6 см и 4 см, а боковое ребро — 8 см. Найти площадь полной поверхности усеченной пирамиды. |
| 2. | Стороны прямоугольника 4 см и 5 см. Найдите площадь полной поверхности тела, полученного при вращении прямоугольника вокруг его меньшей стороны. |
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 23.
| 1. | В прямом параллелепипеде длины сторон основания равны 6 м и 8 м, причем эти стороны образуют угол 300, длина бокового ребра 5 м. Найдите Sполн этого параллелепипеда. |
| 2. |
|
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 24.
| 1. | Основанием прямой призмы ABCDA1B1C1D1 является параллелограмм ABCD со сторонами 6 см и 12 см и углом 60°. Диагональ B1D призмы образует с плоскостью основания угол в 30°. Найдите площадь полной поверхности призмы. |
| 2. |
|
Контрольная работа «Площади поверхностей геометрических тел»
Вариант № 25.
| 1. | Основанием прямой призмы ABCDA1B1C1D1 является параллелограмм ABCD со сторонами 4 см и 4 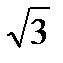см и углом 30°. Диагональ AC1 призмы образует с плоскостью основания угол в 60°. Найдите площадь полной поверхности призмы.
|
| 2. | Высота усеченного конуса 6 см, радиусы его оснований 10 см и 2 см. Вычислите а) площадь боковой поверхности усеченного конуса; б) полной поверхности усеченного конуса. |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|