Контакты

Случайная статья

Треугольник Паскаля. Решение.. Решение.. Домашнее задание.

Треугольник Паскаля

Запишем формулу бинома Ньютона:

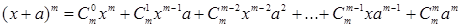
Для того, чтобы каждый раз не вычислять биноминальные коэффициенты по формуле соединений , коэффициенты разложения степени бинома (биноминальные коэффициенты) легко найти по следующей схеме, которая называется «треугольником Паскаля», по имени французского математика Блеза Паскаля.

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

1 6 15 20 15 6 1

1 7 21 35 35 21 7 1

1 8 28 56 70 56 28 8 1

1 9 36 84 126 126 84 36 9 1

1 10 45 120 210 256 210 120 45 10

……………………………………………………

В каждой строчке этой схемы коэффициенты степени бинома, кроме первого и последнего, получаются попарным сложением ближайших коэффициентов предыдущей строки.

При 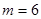имеем строку 1 6 15 20 15 6 1, которая получается из предыдущей строки так:

; ; ; ; .

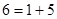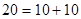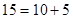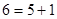Таким образом,

.

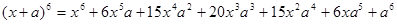Пример 1.Найти разложение бинома .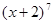

Решение.

.

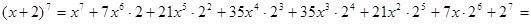
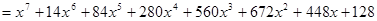Пример 2. Записать разложение бинома: 2) 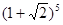; 4) .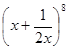

Решение.

2)

.

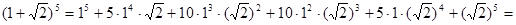
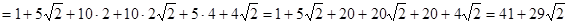4)

.

Домашнее задание.

№ 348.Записать разложение бинома: 1) 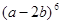; 3) .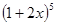

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.