Хелпикс

Главная

Контакты

Случайная статья



Вопросы к зачету по дисциплине «Математический анализ»



Вопросы к зачету по дисциплине «Математический анализ»

1 курс, 1семестр

направление «Экономика»

  1. Множества. Виды числовых множеств.
  2. Понятие функции. Способы задания функции.
  3. Основные свойства функции
  4. Обратная функция, построение графика обратной функции
  5. Основные элементарные функции (степенная, показательная, логарифмическая)
  6. Основные элементарные функции (тригонометрические, обратные тригонометрические)
  7. Элементарные функции. Примеры неэлементарных функций
  8. Последовательность. Предел последовательности.
  9. Теоремы о пределе последовательности
  10. Действия над сходящимися последовательностями
  11. Предел функции
  12. Бесконечные пределы и предел функции при 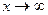. Односторонние пределы.
  13. Бесконечно малые и бесконечно большие величины. Свойства бесконечно малых и бесконечно больших
  14. Сравнение бесконечно малых. Понятие эквивалентности.
  15. Основные теоремы о пределе функции
  16. Замечательные пределы
  17. Непрерывность функции. Основные теоремы о непрерывности функции
  18. Разрывы функции . Классификация разрывов.
  19. Примеры использования функции и ее предела в экономике.
  20. Задачи, приводящие к понятию производной функции
  21. Определение производной функции. Геометрический и механический смысл производной.
  22. Связь между непрерывностью и дифференцируемостью. Таблица производных. Вывод формул для производной постоянной и логарифмической функций.
  23. Основные теоремы о производных..
  24.  Логарифмическая производная., ее экономический смысл. Дифференцирование степенно-показательных функций
  25. Производная неявной функции и функции, заданной параметрически.
  26. Дифференциал функции. Геометрический смысл. Приближенное вычисление значения функции с помощью дифференциала.
  27. Производные и дифференциалы высших порядков
  28. Основные теоремы дифференциального исчисления (теорема Ферма с доказательством)
  29. Основные теоремы дифференциального исчисления (теорема Ролля с доказательством
  30. Основные теоремы дифференциального исчисления (теоремы Коши и Лагранжа с доказательством)
  31. Теорема Лопиталя.. Следствия.
  32. Формула Тейлора
  33. Признаки монотонности функции
  34. Экстремум функции. Необходимое и достаточное условия экстремума.
  35. Выпуклость. Вогнутость. Необходимое и достаточное условия точки перегиба.
  36. Асимптоты. Способы их нахождения
  37. Общий план исследования функций и построения их графиков
  38. Предельные величины в экономике
  39. Использование логарифмической производной в экономике
  40. Эластичность. Ее свойства. Геометрический смысл эластичности.
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.