Тема: Решение простейших задач в координатах

Тема: Решение простейших задач в координатах

Типовые задания:

Задание 1. Даны точки А(1; 2; 3), В(0; 1; 2), С(0; -1; 0), D(1; 2; 0). Какие из этих точек лежат:

1) в плоскости ху;

2) на оси z;

3) в плоскости уz?

Задание 2.В плоскости ху найдите точку D(х; у; 0), равноудаленную от трех данных точек: А(0; 1; -1), В(-1; 0; 1), С(0; -1; 0).

Задание 3.Даны две точки А₁(1; 2; 3), А₂(3; -3; 1). Найдите середину отрезка А₁А₂.

Задание 4.Отрезок АВ задан его серединой М(1; 2; 3) и концом В(-2; 0; 1). Найдите координаты точки А.

Решение типового задания 1:

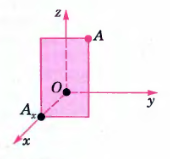Имеем: А(1; 2; 3), В(0; 1; 2), С(0; -1; 0), D(1; 2; 0).

1) У точек плоскости ху координата z равна нулю. Поэтому только точка D(1; 2; 0) лежит в плоскости ху;

2) У точек на оси z две координаты (х и у) равны нулю. Поэтому только точка С(0; -1; 0) лежит на оси z;

3) У точек плоскости уz координата х равна нулю. Следовательно, точки В(0; 1; 2) и С(0; -1; 0) лежат в плоскости уz.

Решение типового задания 2:

Расстояние между точками А₁(х₁; у₁; z₁) и А₂(х₂; у₂; z₂) вычисляется по формуле: .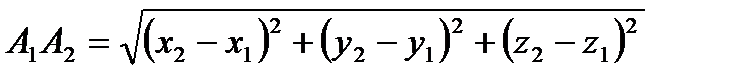

Имеем: AD² = (x – 0)² + (y – 1)² + (0 + 1)²,

BD² = (x + 1)² + (y – 0)² + (0 - 1)²,

CD² = (x – 0)² + (y + 1)² + (0 - 0)².

Приравнивая первые два расстояния третьему, получим два уравнения для определения х и у: -4у + 1 = 0, 2х – 2у +1 = 0.

Отсюда у = 1/4, х = -1/4.

Искомая точка D(-1/4, 1/4, 0

Решение типового задания 3:

Координаты середины отрезка с концами вычисляются по формулам:

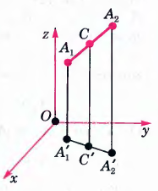
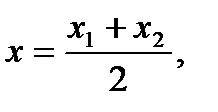
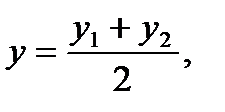
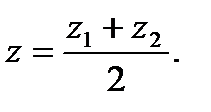
Даны точки А₁(1; 2; 3) и А₂(3; -3; 1). Найдем координаты точки С:

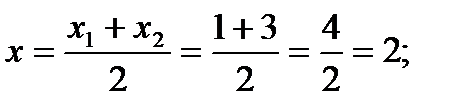
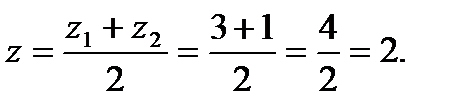
Таким образом, точка С(1; -1/2; 2).

Решение типового задания 4:

Используя формулы нахождения координат середины отрезка, получим формулы для искомой точки А:

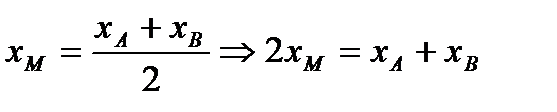или .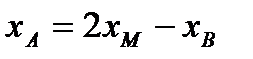

Аналогично, выводятся формулы: 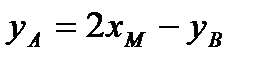и .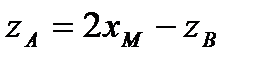

Таким образом,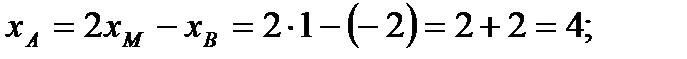

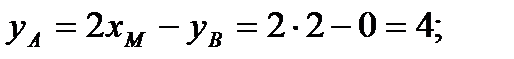
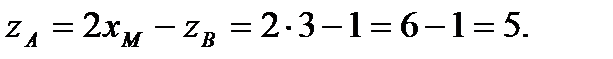
Окончательно, искомая точка А(4; 4; 5)