
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Посмотри видео урок по теме «Формулы приведения» по ссылке videouroki.net
Задание по алгебре для 101 группы за 25 мая
1. Посмотри видео урок по теме «Формулы приведения» по ссылке videouroki.net
2.Изучи теоретический материал по теме«Формулы приведения»
Для вычисления углов больше 90  используют формулы приведения. Они позволяют синус, косинус, тангенс и котангенс различных углов приводить к острым углам.
используют формулы приведения. Они позволяют синус, косинус, тангенс и котангенс различных углов приводить к острым углам.
Пример: Вычислить 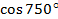 и
и 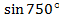 .
.
Представим число 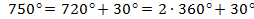 .
.
Рассмотрим точку А(1;0) на единичной окружности. При повороте вокруг начала координат на угол 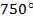 она сделает 2 полных оборота
она сделает 2 полных оборота  и ещё повернётся на угол
и ещё повернётся на угол 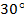 . Переместится в точку В, в которую могла бы попасть, сделав поворот на угол
. Переместится в точку В, в которую могла бы попасть, сделав поворот на угол 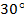 . Значит,
. Значит, 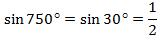 ,
, 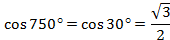 .
.
А так как  , то
, то 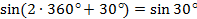 ,
, 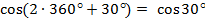
Количество полных оборотов по 360  или по
или по 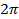 может выражаться любым целым числом k, как положительным, так и отрицательным и нулём. При повороте точки А(1;0) на угол
может выражаться любым целым числом k, как положительным, так и отрицательным и нулём. При повороте точки А(1;0) на угол  , где k
, где k 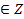 получается та же самая точка, что при повороте на угол
получается та же самая точка, что при повороте на угол 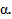
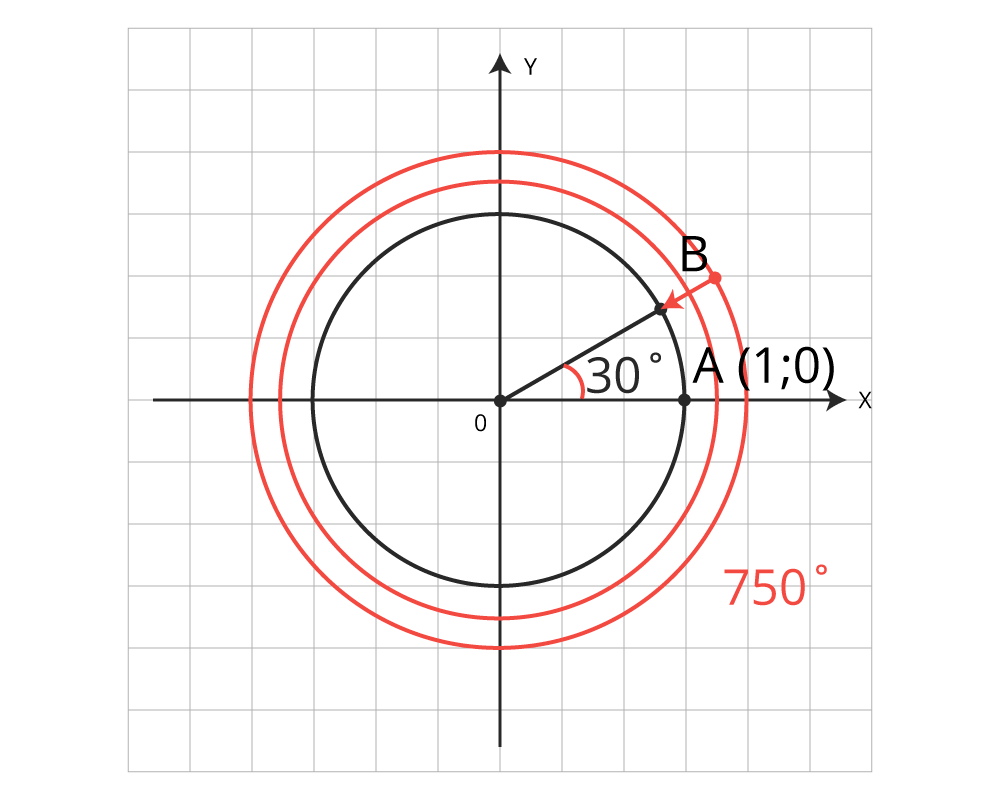
Рисунок 1 – точки А и В на
единичной окружности
Т.е. справедливы равенства:
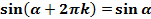 , где
, где 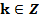 ,
,
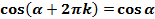 , где
, где 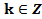
Пусть точка А(1;0) переместилась в точку В1 при повороте на угол 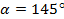 и в точку В при повороте на угол
и в точку В при повороте на угол 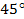 (рис. 2).
(рис. 2).
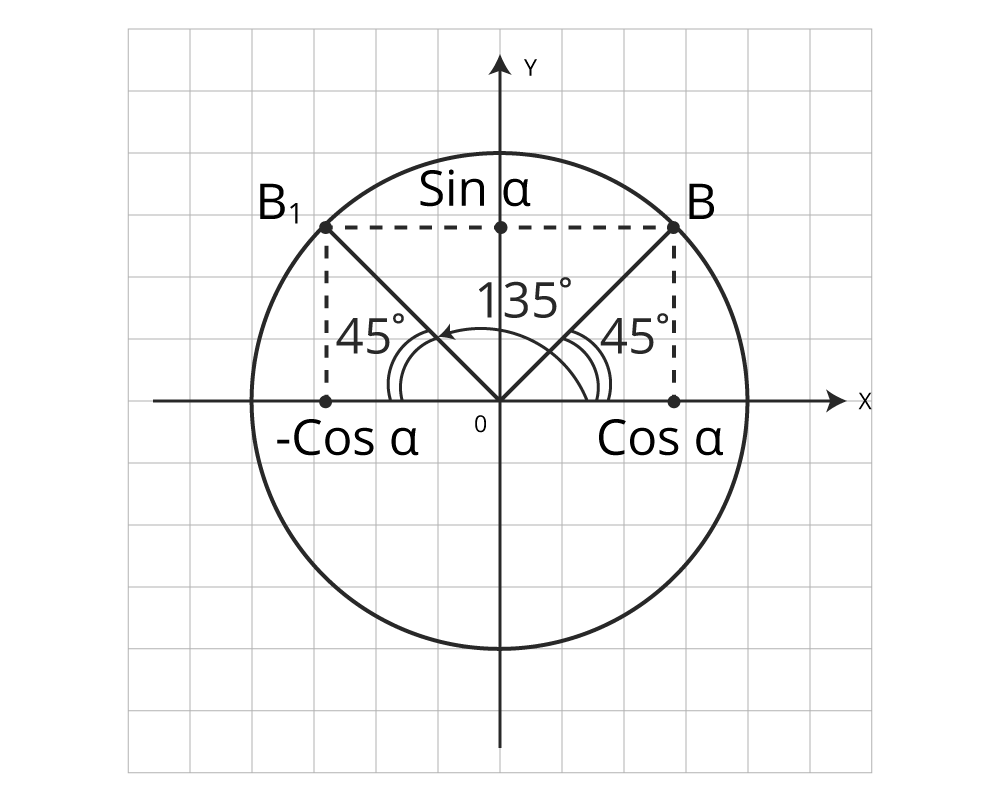
Рисунок 2 – точки А, В, В1 на единичной окружности
Запишем 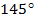 в виде:
в виде: 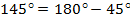 . На единичной окружности точки В1 и В симметричны относительно оси Оу, значит их ординаты (синусы) равны, абсциссы (косинусы)- противоположные числа.
. На единичной окружности точки В1 и В симметричны относительно оси Оу, значит их ординаты (синусы) равны, абсциссы (косинусы)- противоположные числа.
Поэтому  , а
, а 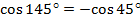 .
.
А так как 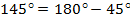 , то
, то 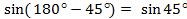 ,
, 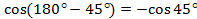 .
.
Помним, что 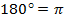 , тогда
, тогда 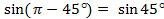 ,
, 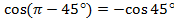 .
.
Докажем, что для всех углов 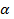 справедливы формулы:
справедливы формулы:
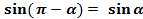 ,
, 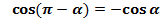 .
.
Воспользуемся формулой синуса и косинуса разности: 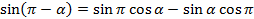 , подставим известные значения
, подставим известные значения 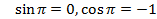 в формулу, получаем:
в формулу, получаем:
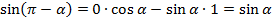 .
.
 (1)
(1)
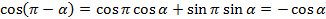
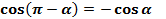 (2)
(2)
Аналогично доказываются формулы:
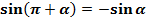 (3) ;
(3) ; 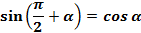 (4) ;
(4) ; 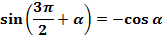 (5)
(5)
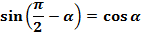 (6);
(6); 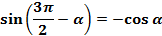 (7)
(7)
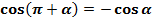 (8);
(8); 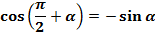 (9);
(9); 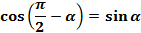 (10)
(10)
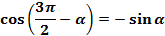 (11);
(11); 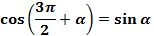 (12)
(12)
Эти формулы называются формулами приведения для синуса и косинуса.
Пример: вычислите  . Представим
. Представим  , тогда
, тогда  .
.
Выведем формулы для тангенса, используя его определение
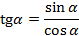 ,
,
Найдём 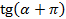
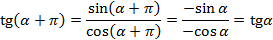

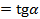
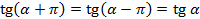
Получаем формулы для тангенса и котангенса:
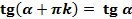 , где
, где 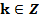 и
и 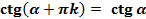 , где
, где 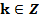 (13)
(13)
 (14);
(14); 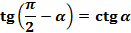 (15)
(15)
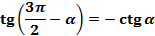 (16);
(16); 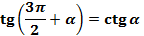 (17)
(17)
Пример: вычислите 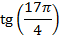 .
.
Преобразуем выражение в скобке 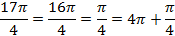
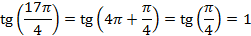 .
.
Обратите внимание, что все эти формулы связывают синусы с синусами или косинусами, а тангенсы с тангенсами или котангенсами. В одних случаях синус меняется на косинус и наоборот, в других – нет. Так, например, в формулах 1,2,3,8 и 13, где в левой части присутствуют 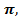 синусы, косинусы и тангенсы не меняются.
синусы, косинусы и тангенсы не меняются.
В остальных формулах, где в левой части присутствуют  или
или 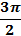 , синус меняется на косинус и наоборот, а тангенс на котангенс.
, синус меняется на косинус и наоборот, а тангенс на котангенс.
Формул приведений много и их не обязательно каждый раз выводить и запоминать.
Для этого придумали правило.
1. Если в левой части присутствуют  и т.д. синусы, косинусы и тангенсы не меняются.
и т.д. синусы, косинусы и тангенсы не меняются.
Если в левой части присутствуют  или
или 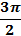 , синус меняется на косинус, косинус на синус, тангенс на котангенс.
, синус меняется на косинус, косинус на синус, тангенс на котангенс.
1. Знак в правой части ставим тот же, который имело исходное число в левой части, при условии 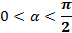 .
.
Существует легенда про рассеянного математика, который всё время забывал менять или не менять синус на косинус и наоборот. Он смотрел на свою сообразительную лошадь и она кивала головой вдоль той оси, где стояли числа  и
и 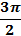 ,
, 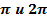 .(рис. 3)
.(рис. 3)
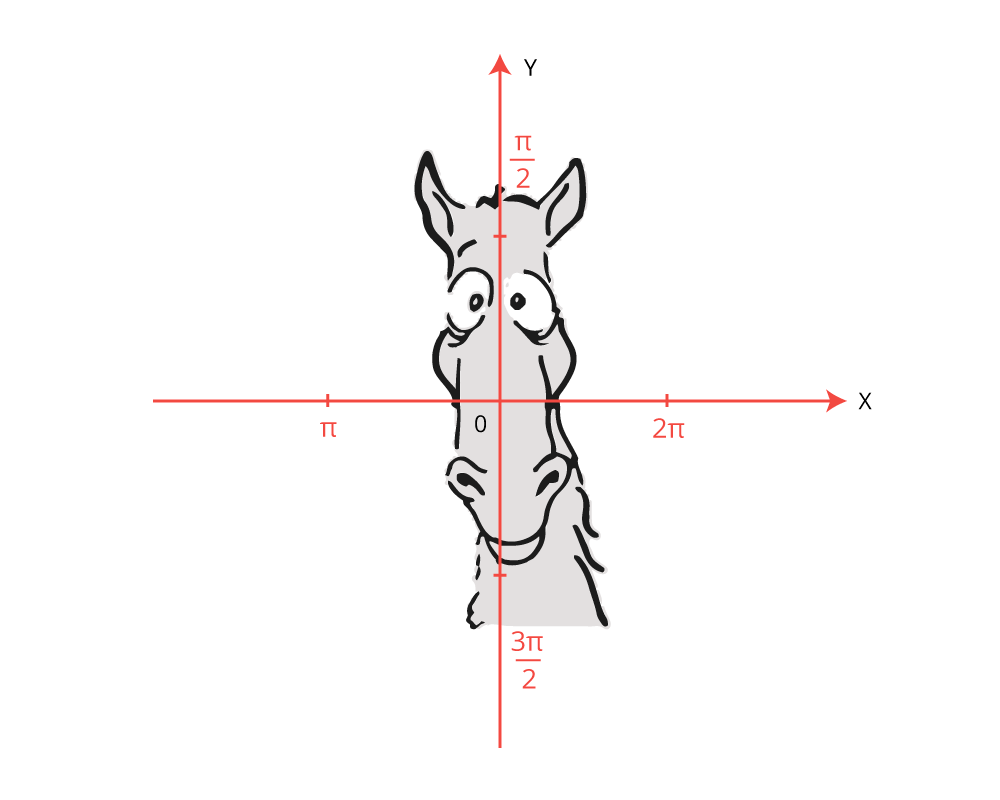
Рисунок 3 – «правило лошади»
Если аргумент содержал 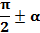 или
или 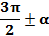 , лошадь кивала вдоль оси Оу. Это означало «да, менять». А если
, лошадь кивала вдоль оси Оу. Это означало «да, менять». А если 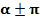 , кивала вдоль оси Ох – «не менять».
, кивала вдоль оси Ох – «не менять».
Так же помните: чётные числа вида 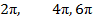 и т.д. находятся на оси Ох справа от нуля на единичной окружности, а нечётные
и т.д. находятся на оси Ох справа от нуля на единичной окружности, а нечётные 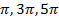 и т. д. слева от нуля.
и т. д. слева от нуля.
Если в выражении перед 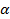 стоит плюс, то точка перемещается по окружности по часовой стрелке, если стоит минус, то против часовой стрелке.
стоит плюс, то точка перемещается по окружности по часовой стрелке, если стоит минус, то против часовой стрелке.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|