
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Системы линейных неравенств. Системы неравенств с одной переменной
Системы линейных неравенств. Системы неравенств с одной переменной
Напомним некоторые сведения о системе неравенств. Итак, пусть нам надо найти все значения переменной икс, которые являются решениями каждого из неравенств 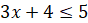 и
и 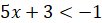 .
.
Говорят, что надо решить систему неравенств:
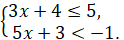
Записанная система неравенств является примером системы из двух линейных неравенств с одной переменной (с одним неизвестным).
Значения переменной, которые являются решениями каждого неравенства системы, называются решениями системы. Решить систему неравенств – это значит найти все её решения или доказать, что их нет.
Две системы неравенств называются равносильными, если каждое решение первой системы является решением второй системы, и наоборот – каждое решение второй системы является решением первой системы, то есть если они имеют одни и те же решения. Равносильными называются и системы, которые не имеют решений.
Мы с вами повторили основные моменты, а теперь давайте перейдём к практической части занятия.
Задание первое. Решите системы неравенств:
а) 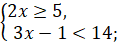
б) 
в) 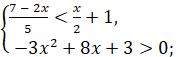
г) 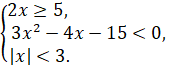
Решение.

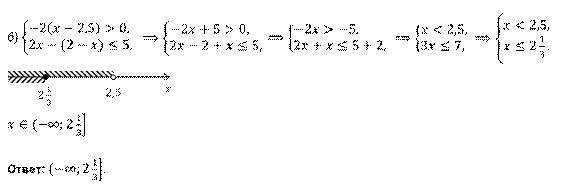
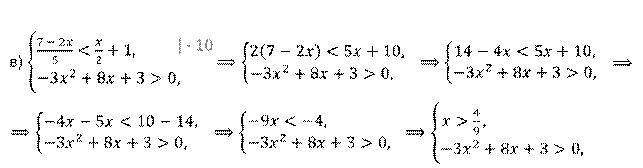

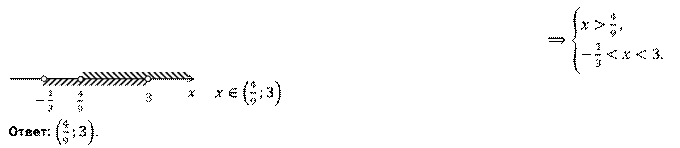

Задание второе. Решите системы неравенств:
а) 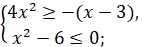
б) 
Решение.
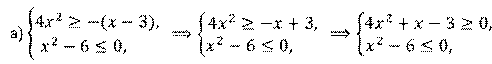



Задание третье. Решите систему неравенств: 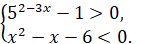 .
.
Решение.
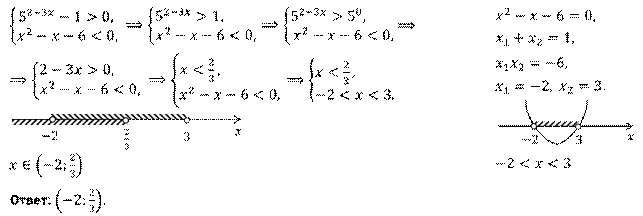
Задание четвёртое. Решите систему неравенств:  .
.
Решение.
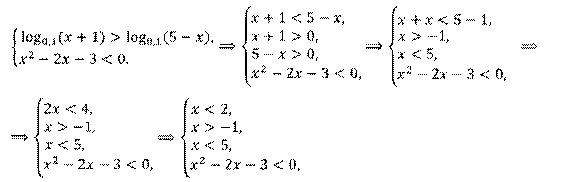

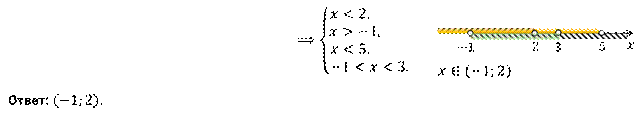
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|