
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Уравнение плоскости
Уравнение плоскости
План
1. Уравнение плоскости
2. Расстояние от точки до плоскости
3. Примеры
Вопрос 1. Уравнение плоскости
Уравнение с тремя переменными x, у, z называетсяуравнением данной поверхности P в системе координат Охуz, если этому уравнению удовлетворяют координаты любой точки поверхности Р и не удовлетворяют координаты никакой точки, не лежащей на этой поверхности.
Пусть дана некоторая точка M0(x0;y0;z0) и ненулевой вектор 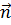 . Через точку M0 можно провести только одну плоскость α перпендикулярную вектору
. Через точку M0 можно провести только одну плоскость α перпендикулярную вектору 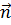 .
.
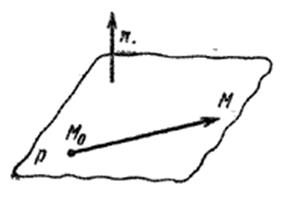
Выведем уравнение плоскости α. Пусть М — произвольная точка пространства. Очевидно, что точка М принадлежит плоскости α только тогда, когда вектор 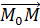 перпендикулярен вектору
перпендикулярен вектору 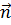 . Поэтому уравнение плоскости, проходящей через точку M0 перпендикулярно вектору
. Поэтому уравнение плоскости, проходящей через точку M0 перпендикулярно вектору 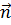 , можно записать в виде:
, можно записать в виде: 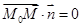 . Вектор
. Вектор 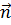 в уравнении называется нормальным вектором плоскости. В качестве нормального вектора можно взять любой вектор, перпендикулярный плоскости.
в уравнении называется нормальным вектором плоскости. В качестве нормального вектора можно взять любой вектор, перпендикулярный плоскости.
Пусть координаты вектора 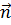 равны
равны 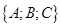 . И обозначим координаты произвольной точки М через x, y и z. Тогда вектор
. И обозначим координаты произвольной точки М через x, y и z. Тогда вектор 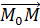 имеет координаты
имеет координаты 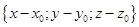 .
.
Теперь можно записать уравнение плоскости через координаты вектора 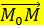 и вектора
и вектора 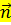 :
:
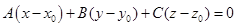
Это уравнение называется уравнением плоскости, проходящей через точку M0(x0;y0;z0) перпендикулярно вектору 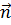 (А; В; С). Раскроем скобки и перегруппируем слагаемые, обозначив слагаемые, не содержащие переменные за D:
(А; В; С). Раскроем скобки и перегруппируем слагаемые, обозначив слагаемые, не содержащие переменные за D:
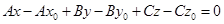 ;
;
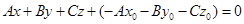 ;
;
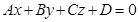 .
.
Вопрос 2. Расстояние от точки до плоскости
Рассмотрим плоскость α и точку А, которая лежит вне этой плоскости. Как известно, из точки А можно провести единственную прямую АH перпендикулярную плоскости α. Проведем прямую АН перпендикулярно плоскости α, 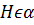 .
.
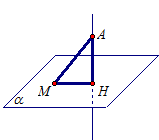
Расстоянием от точки А до плоскости α называют длину перпендикуляра АН. Обозначают ρ(А; α) = АН. Заметим, что АН – наименьшее из расстояний между точкой А и любой точкой плоскости. Действительно, в прямоугольном треугольнике АНМ перпендикуляр (катет АН) короче наклонной (гипотенузы АМ).
Расстояние между параллельными плоскостями
Плоскость α и плоскость β параллельны. На плоскости β выберем произвольную точку А.
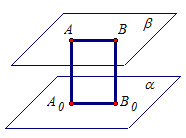
Из точки А опустим перпендикуляр АА0 на плоскость α. Перпендикуляр АА0 и назовем расстоянием между плоскостями α и β.
Заметим, что длина этого перпендикуляра не зависит от того, какую точку мы выбрали.
Например, выберем другую точку В, опустим перпендикуляр ВВ0. Прямые АА0 и ВВ0 перпендикулярны одной и той же плоскости, значит, прямые АА0 и ВВ0 параллельны. Тогда из свойств параллельных плоскостей отрезки АА0 и ВВ0 равны.
Расстояние между прямой и плоскостью
Расстояние между прямой и плоскостью определяется в случаях, когда прямая параллельна плоскости. Тогда все точки прямой а равноудалены от плоскости α. Выберем любую точку А на прямой а, опустим перпендикуляр АА0 на плоскость α.
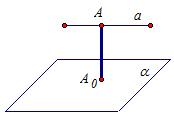
Длина перпендикуляра АА0 и называется расстоянием между прямой а и параллельной ей плоскостью α. Обозначение: АА0 = р(а; α).
Вопрос 3.Примеры
Пример 1. Составить уравнение плоскости, проходящей через точку 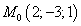 и перпендикулярной вектору
и перпендикулярной вектору 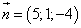 .
.
Решение. Используем формулу : 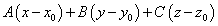 =0.
=0.
В этой формуле числа A, B и C координаты вектора 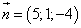 , а числа x0, y0 и z0 - координаты точки
, а числа x0, y0 и z0 - координаты точки 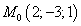 .
.
Подставляем эти числа в формулу и получаем
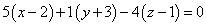 .
.
Раскроем скобки, преобразуем и получим:
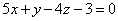 .
.
Требуемое уравнение плоскости в этом примере оказалось выражено общим уравнением первой степени относительно переменных координат x, y, z произвольной точки плоскости.
Итак, уравнение вида
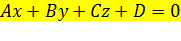
называется общим уравнением плоскости.
Пример 2. Найти уравнение плоскости, проходящей через точку А(1,2,3), перпендикулярной к прямой АВ, если В(2,-1,3).
Решение. Найдём нормальный вектор. В данном случае 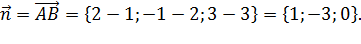 Составим уравнение плоскости
Составим уравнение плоскости
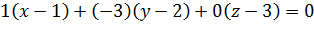
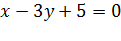
Пример 3. Найдите расстояние от точки С(7,-8,9) до плоскости из предыдущей задачи.
Решение. Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из неё на заданную плоскость и вычисляется по формуле:
 .
.
Подставим координаты точки 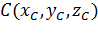 и вектора
и вектора 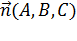 :
:
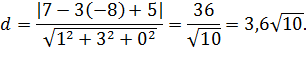
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|