
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вариант – 1. Задания уровня А. Чему равна производная 1?. Назовите формулу, раскрывающую геометрический смысл производной.. Какая из формул задает (u·v)'?. Вычислите ((х-1)5)'.. Найдите производную функции f(x)=2х2-3𝑥+1 в точке х0=1.. Вычислите (х
Тест
по теме: «Производная»
Вариант – 1
Задания уровня А
1. Чему равна производная 1?
1) 1
2) 0
3) х
4) а(число)
2. Назовите формулу, раскрывающую геометрический смысл производной.
1) y=kx + b
2) k=f'(x)
3) y-y0=k(x-x0)
4) y=f (x)
3. Вычислите (6х3)'
1) 6х2
2) 0
3) 18х2
4) 18х
4. Вычислите ( 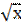 )'
)'
1) 2 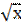
2) х2
3) 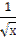
4) 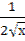
5. Какая из формул задает (u·v)'?
1) u'·v'
2) u'·v-u·v'
3) u'·v+u·v'
4) u'·v'-u·v
6. Вычислите ((х-1)5)'.
1) (х - 4)4
2) 5 (х-1)4
3) 5 (х-1)
4) 5
7. Найдите производную функции f(x)=2х2-3𝑥+1 в точке х0=1.
1) 8
2) 3
3) 7
4) 2
8. Вычислите (х3 + 2х4 - х)'.
1) 3х2 + 2х3 – х
2) 3х2 + 8х3 – х2
3) 3х4 + 8х4 – х2
4) 3х2 + 8х3 – 1
9. Найдите производную функции y=x· .
1) y' = 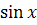
2) y' = 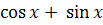
3) y' = 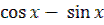
4) y' = 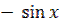
10. Найдите производную функции y = x5 - + 2.
1) y' = 5x - 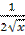 + 2
+ 2
2) y' = 5x4 - 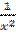 + 2
+ 2
3) y' = 5x4+ 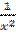
4) y' = 5x4- 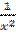
11. Найдите производную функции y = ex +2x4.
1) y' = ex +8x
2) y' = xex-1 +4x3
3) y' = xex-1 +8x3
4) y' = ex +8x3
12. Найдите производную функции y = 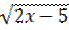 /
/
1) y' = 2
2) y' = 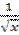
3) y' = 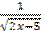
4) y' = 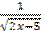
Тест
по теме: «Производная»
Вариант – 2
Задания уровня А
1. Чему равна производная 0?
1) 1
2) 0
3) а
4) х
2. Назовите формулу, раскрывающую механический смысл производной.
1) y = f '(x)
2) k = f '(x)
3) 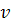 (t)=S'(t)
(t)=S'(t)
4) S(t)= 
3. Вычислите производную (5x4).
1) 5x3
2) 20x3
3) 0
4) 20x
4. Вычислите ( )'.
1) ctg x
2) 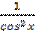
3) 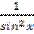
4) − 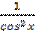
5. Какая из формул задает .
1) 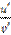
2) u' 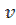 + u
+ u 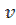 '
'
3) 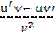
4) u' 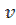 - u
- u 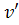 .
.
6. При каком условии функция возрастает?
1) f '(x) = 0
2) f '(x) < 0
3) f '(x) = f (x)
4) f '(x) > 0
1)
7. Вычислите(cos (5x + 1)) '.
1) 5sin x
2) 5cos (x + 1)
3) – 5sin (5x + 1)
4) 5sin (5x + 1)
8. Найдите производную функцииy = x2 + x в точке x0=2.
1) 5
2) 6
3) 4
4) 3
9. Вычислите (2x10 – 3x5 + 3) '.
1) 20x – 15
2) 2x3 – 3x4
3) 20x3 – 15x4 + 3
4) 20x9 – 15x4
10. Найдите производную функции y = .
1) cosx
2) 0
3) 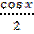
4) sinx
11. Найдите производную функцииy = 1.
1) 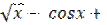 1
1
2) 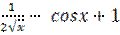
3) 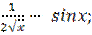
4) 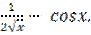
12. Вычислите (2ex + 3) .
1) 2ex + 1
2) ex
3) 2ex
4) 0
13. Найдите производную функцииy = e2x + 1.
1) e2x
2) 2 e2x + 1
3) e2x + 1
4) ex
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|