
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Повторение. Неравенства.
Тема: Повторение. Неравенства.
Цель: Повторить способы решения неравенств, подготовиться к экзамену.
Что повторяем:
1) показательные неравенства;
2) логарифмические неравенства;
3) тригонометрические неравенства.
Теоретический материал для повторения.
Показательными называются неравенства, у которых переменная содержится в показатели степени. 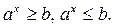
Логарифмические неравенства — это неравенства, в которых переменная величина находится под знаком логарифма.
Тригонометрические неравенства – это неравенства, в которых переменная находится под знаком тригонометрической функции.
С решениями всех этих неравенств мы с вами уже знакомы. Наша задача обобщить и привести знания в систему. Начнем с показательных неравенств.
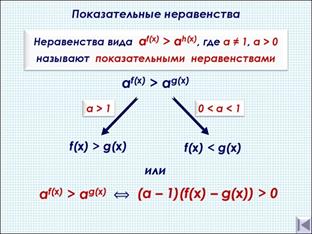
При решении показательных неравенств, обращаем внимание на основание. Если а>1, то знак неравенства сохраняется. Если 0<а<1, то знак неравенства меняется.



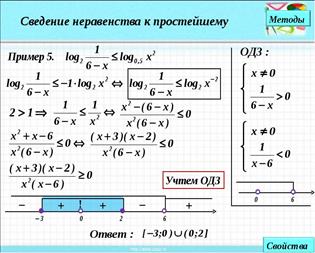
Решая логарифмические неравенства, сравниваем основание логарифма с единицей: если а>1, то знак неравенства сохраняется, а если 0<а<1,то знак неравенства меняется. При решении логарифмических неравенств обращаем внимание на область допустимых значений. Затем с учетом ОДЗ и значения решаем неравенство.




Рассмотрим методы решения. Основных приема два: приведение к одинаковому знаменателю и замена переменной.
1.Как в показательном, так и в логарифмическом уравниваем основания. Затем сравним показатели или числа, стоящие под знаком логарифма.
2. Замена переменных.
Находим корни и делаем обратную замену. При решении неравенств, применяем те же самые приемы.
При решении логарифмических уравнений, возможно появление посторонних корней. Причина их появления — расширение области определения исходного уравнения. Поэтому проверка корней логарифмического уравнения осуществляется либо по области определения, либо непосредственной подстановкой найденных корней в исходное логарифмическое уравнение.

Тригонометрические неравенства – это неравенства вида 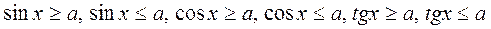



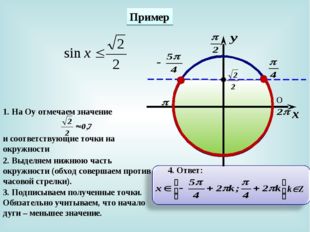


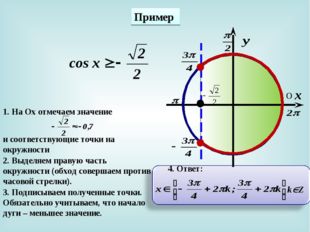
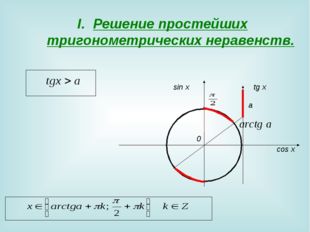
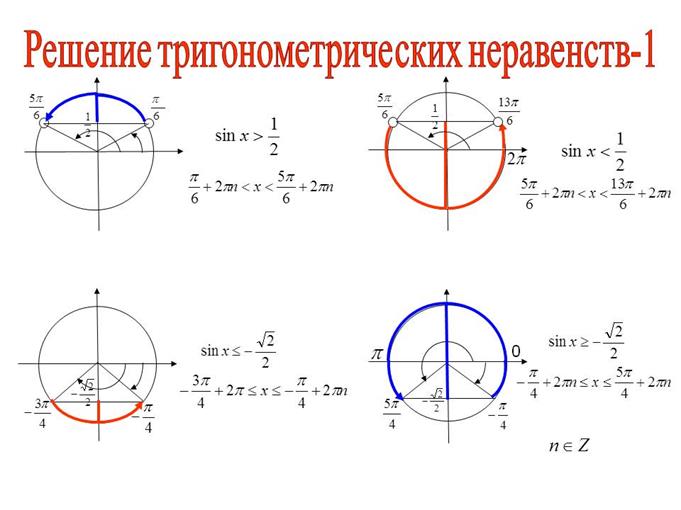
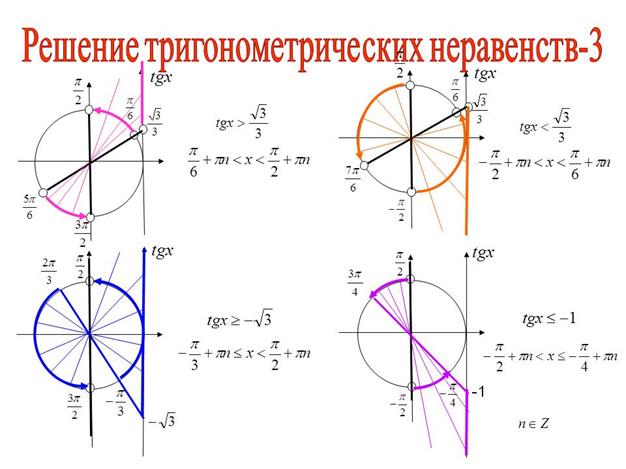
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|