
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема 4. Тригонометрические уравнения
Тема 4. Тригонометрические уравнения
Простейшие тригонометрические уравнения имеют следующие решения:
1) 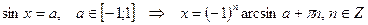 ;
;
2) 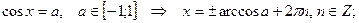
3) 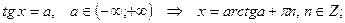
4) 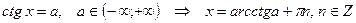 .
.
Пример 1. Решите уравнение 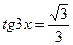 .
.
1) 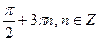 2)
2) 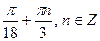 3)
3) 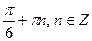 4)
4) 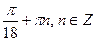
Решение. 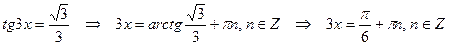
Получаем 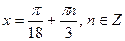
Ответ: 2).
Пример 2. Решите уравнение 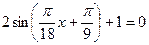 .
.
1) 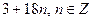 2)
2) 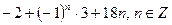
3) 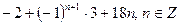 4)
4) 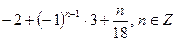
Решение. 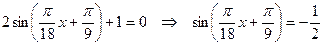 .
.
Так как 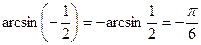 , то уравнение имеет решение:
, то уравнение имеет решение:
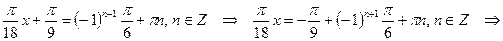
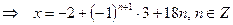 .
.
Ответ: 3).
Пример 3. Укажите наименьший положительный корень уравнения 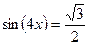 .
.
Решение. 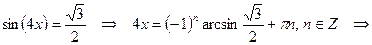
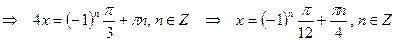 .
.
Наименьший положительный корень уравнения получаем при n=0: 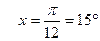 .
.
Ответ: 15.
Частные случаи:
1) 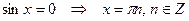
2) 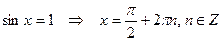
3) 
4) 
5) 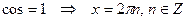
6) 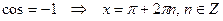
7) 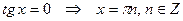
8) 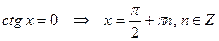
Пример 4. Решите уравнение 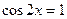 .
.
Решение. Используем формулу 5 для частных случаев:
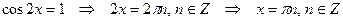 .
.
Ответ: 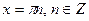
Тригонометрические уравнения, которые не являются простейшими, часто решаются разложением левой части уравнения на множители. При этом применяются тригонометрические формулы.
Пример 5. Решите уравнение 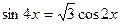 .
.
Решение. Применим формулу синуса двойного угла:
 .
.
Это уравнение равносильно совокупности уравнений: 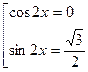 .
.
1) 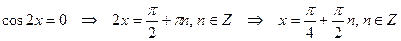
2) 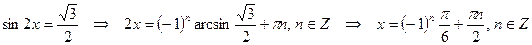
Ответ: 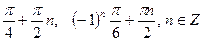 .
.
Задачи.
1. Решите уравнение 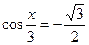 .
.
1) 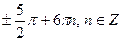 2)
2) 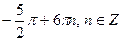 3)
3) 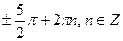 4)
4) 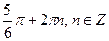
2. Решите уравнение 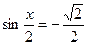 .
.
1) 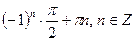 2)
2) 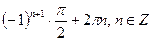
3) 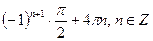 4)
4) 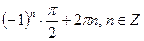
3. Решите уравнение 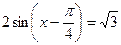 .
.
4. Решите уравнение 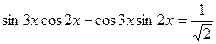 .
.
1) 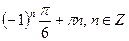 2)
2) 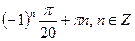 3)
3) 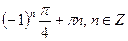 4)
4) 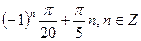
5. Решите уравнение 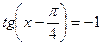 и найдите корни, расположенные на промежутке
и найдите корни, расположенные на промежутке 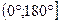 . Ответ приведите в градусах.
. Ответ приведите в градусах.
6. Решите уравнение 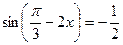 и найдите корни, расположенные на промежутке
и найдите корни, расположенные на промежутке 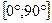 . Ответ приведите в градусах.
. Ответ приведите в градусах.
7. Решите уравнение 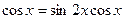 и найдите корни, расположенные на промежутке
и найдите корни, расположенные на промежутке 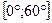 . Ответ приведите в градусах.
. Ответ приведите в градусах.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|