
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема 3. Обратные тригонометрические функции
Тема 3. Обратные тригонометрические функции
Определения 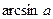 ,
, 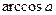 ,
, 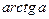 ,
, 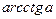
| 1. | 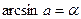 , если , если 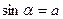 , , 
| Арксинусом числа a называется такое число из отрезка 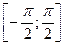 , синус которого равен a. , синус которого равен a.
|
| 2. | 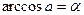 , если , если 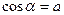 , , 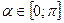
| Арккосинусом числа a называется такое число из отрезка 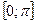 , косинус которого равен a. , косинус которого равен a.
|
| 3. | 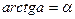 , если , если 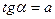 , , 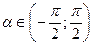
| Арктангенсом числа a называется такое число из интервала 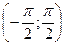 , тангенс которого равен a. , тангенс которого равен a.
|
| 4. | 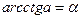 , если , если 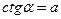 , , 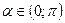
| Арккотангенсом числа a называется такое число из интервала 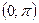 , котангенс которого равен a. , котангенс которого равен a.
|
Основные тождества:
1. 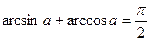 , , 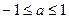 2.
2. 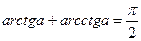 , , 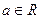 3.
3. 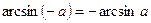 , , 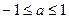
|
4. 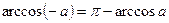 , , 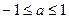 5.
5. 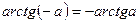 , , 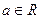 6.
6. 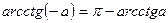 , , 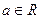
|
Пример 1.Вычислите в градусах значение выражения 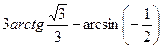 .
.
Решение. Находим значения обратных тригонометрических функций, используя их определения: 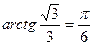 , так как
, так как 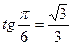 и
и 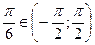 ;
; 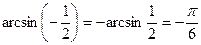 , так как
, так как 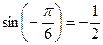 и
и 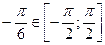 . Тогда
. Тогда 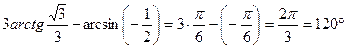 .
.
Ответ: 120.
Пример 2. Укажите в градусах значение угла 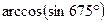 .
.
Решение. Вычисляем, используя периодичность функции 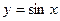 , значение
, значение 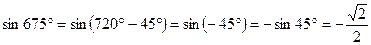 . Тогда, применяя основное тождество 4, получаем:
. Тогда, применяя основное тождество 4, получаем: 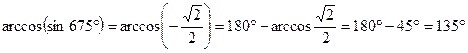 .
.
Ответ: 135.
Из определений значений обратных тригонометрических функций вытекают следующие соотношения:
1. 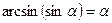 , если , если  2.
2. 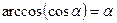 , если , если 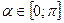
| 3. 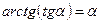 , если , если 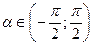 4.
4. 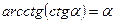 , если , если 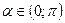
|
Пример 3. Укажите в градусах значение угла 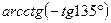 .
.
Решение. Применяем формулу приведения и соотношение 3:
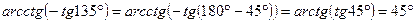 .
.
Ответ: 45.
Рассмотрим свойства и графики обратных тригонометрических функций 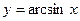 ,
, 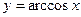 ,
, 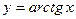 ,
, 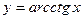 .
.
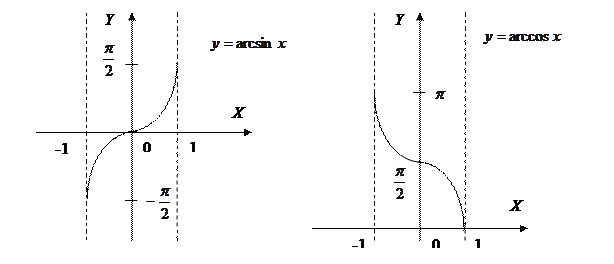
| Свойства функции 1. 2. 3. Функция возрастает на промежутке | Свойства функции 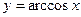 :
1. :
1. 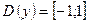 .
2. .
2. 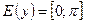 .
3. Функция убывает на промежутке .
3. Функция убывает на промежутке 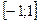 . .
| ||
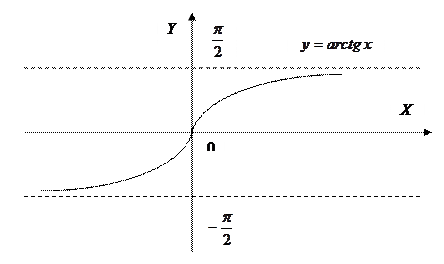
Свойства функции 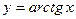 :
1. :
1. 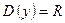 .
2. .
2. 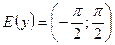 .
3. Функция возрастает на R. .
3. Функция возрастает на R.
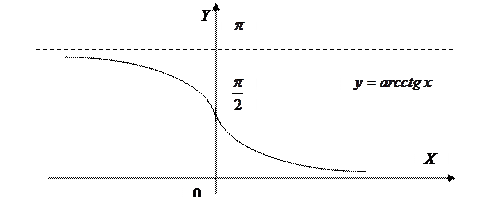
| Свойства функции 1. 2. 3. Функция убывает на R.
| ||
Из определений обратных тригонометрических функций и соотношений между тригонометрическими функциями одного и того же аргумента вытекают следующие тождества, справедливые в области определения соответствующих функций:
1. 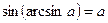
2. 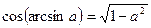
3. 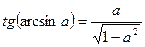
4. 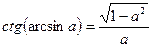
5. 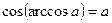
6. 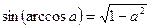
7. 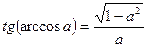
8. 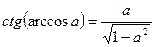
9. 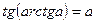
10. 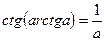
11. 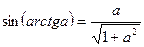
12. 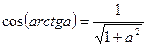
13. 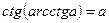
14. 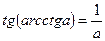
15. 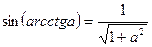
16. 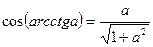
Пример 4. Вычислите 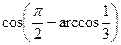 .
.
1) 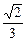
2) 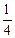
3) 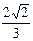
4) 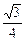
Решение. По формуле приведения и тождеству 5 получаем:
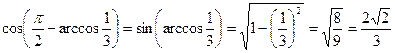 .
.
Ответ: 3).
Пример 5. Результат вычисления выражения 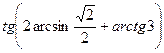 равен
равен
1) 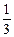 2) 3 3) -3 4)
2) 3 3) -3 4) 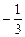
Решение. Так как 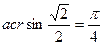 , применяем формулу приведения и тождество 10:
, применяем формулу приведения и тождество 10:
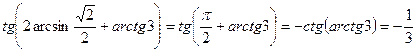 .
.
Ответ: 4).
Пример 6. Результат вычисления выражения 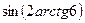 равен
равен
1) 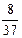
2) 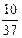
3) 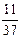
4) 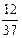
Решение. Используем формулу для синуса двойного угла и тождества 11, 12:
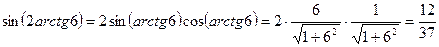 .
.
Ответ: 4).
Задачи.
1. Вычислите в градусах значения следующих выражений:
1) 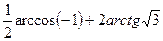
2) 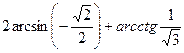
3) 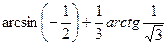
4) 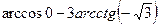
2. Укажите в градусах значения углов:
1) 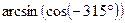
2) 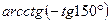
3) 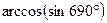
4) 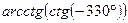
3. Результат вычисления выражения 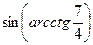 равен
равен
1) 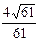
2) 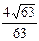
3) 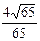
4) 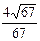
4. Результат вычисления выражения 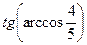 равен
равен
1) 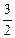
2) 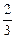
3) 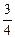
4) 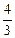
5. Результат вычисления выражения 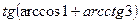 равен
равен
1) 3
2) 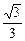
3) 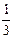
4) 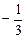
6. Результат вычисления выражения 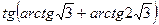 равен
равен
1) 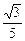
2) 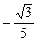
3) 
4) 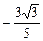
7. Результат вычисления выражения 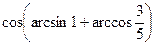 равен
равен
1) 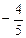
2) 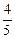
3) 
4) 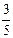
8. Результат вычисления выражения 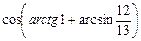 равен
равен
1) 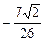
2) 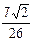
3) 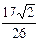
4) 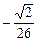
9. Результат вычисления выражения 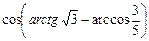 равен
равен
1) 
2) 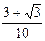
3) 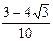
4) 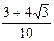
10. Результат вычисления выражения 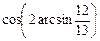 равен
равен
1) 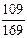
2) 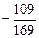
3) 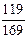
4) 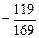
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
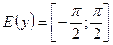 .
. .
.