
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 37. Краткие теоретические сведения
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 37
Тема:Нахождение значений обратных тригонометрических функций (арксинус, арккосинус, арктангенс, арккотангенс)
Краткие теоретические сведения

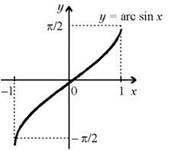

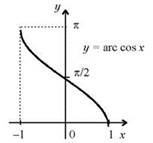

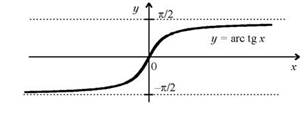

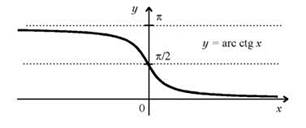
Пример 1. Вычислить:
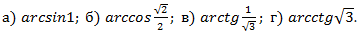
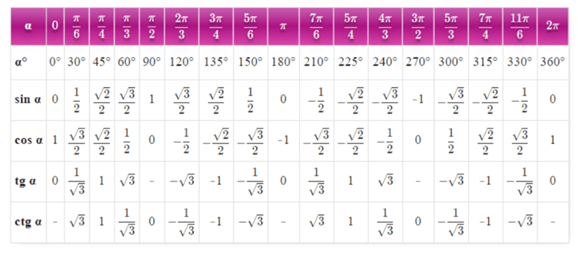
Решение: Как видим, все аргументы аркфункций положительные и табличные, а это значит, что мы можем восстановить значение углов по первой части таблицы значений тригонометрических функций для углов от 0° до 90°. Этот диапазон углов входит в область значений каждой из аркфункций, поэтому просто пользуемся таблицей, находим в ней значение тригонометрической функции и восстанавливаем, какому углу оно соответствует.
а) 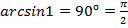 б)
б) 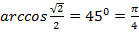
в) 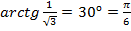 г)
г) 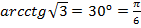
Пример 2. Вычислить:
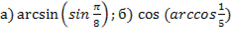
Решение: Воспользуемся основными свойствами указанных аркфункций, только обязательно проверяя при этом соответствующие им ограничения.
а) 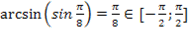 б)
б) 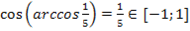 .
.
Пример 3. Вычислить
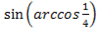
Решение:
В указанном примере мы имеем дело с выражением, которое похоже на основное свойство арксинуса, но только в нем присутствуют кофункции. Его надо привести к виду синус от арксинуса или косинус от арккосинуса. Поскольку преобразовывать прямые тригонометрические функции проще, чем обратные, перейдем от синуса к косинусу с помощью формулы «тригонометрической единицы».
Как мы уже знаем:
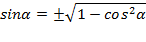
В нашем случае в роли 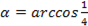 . Вычислим для удобства сначала
. Вычислим для удобства сначала 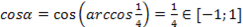
Перед подстановкой его в формулу выясним ее знак, т.е. знак исходного синуса. Синус мы должны вычислить от значения арккосинуса, каким бы это значение ни было, мы знаем, что оно лежит в диапазоне 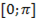 . Этому диапазону соответствуют углы первой и второй четвертей, в которых синус положителен (проверьте это сами с помощью тригонометрической окружности).
. Этому диапазону соответствуют углы первой и второй четвертей, в которых синус положителен (проверьте это сами с помощью тригонометрической окружности).
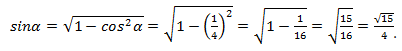
Содержание работы
Вариант 1
Задание 1.Вычислить: 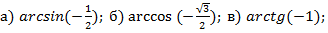
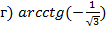 .
.
Задание 2.Вычислить: 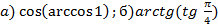 .
.
Задание 3.Вычислить: 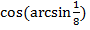
Вариант 2
Задание 1.Вычислить: 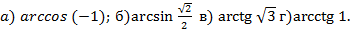
Задание 2.Вычислить: 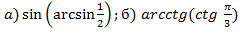 .
.
Задание 3.Вычислить: 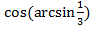
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|