Контакты

Случайная статья

Практическая работа № 36. Тема: Вычисление определённого интеграла. Площадь криволинейной трапеции.. Цель: Применение знаний при решении задач.. Теория. Задача 2

Практическая работа № 36

Тема: Вычисление определённого интеграла. Площадь криволинейной трапеции.

Цель: Применение знаний при решении задач.

Теория

Опр.

Если F(x) - первообразная функции f(x) , то разность F(b) - F(а) называется определённым интегралом от функции f(x) на отрезке [a ; b] и обозначают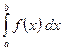

а – нижний предел интегрирования

b - верхний предел интегрирования

f(x)- подынтегральная функция

Правило вычисления определённого интеграла:

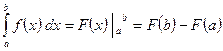Формула Ньютона – Лейбница

Примеры:

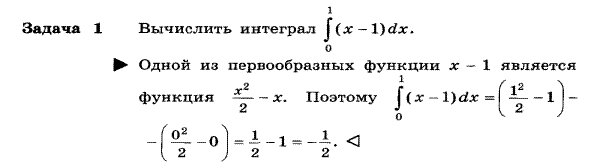
Задача 2

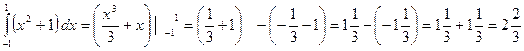
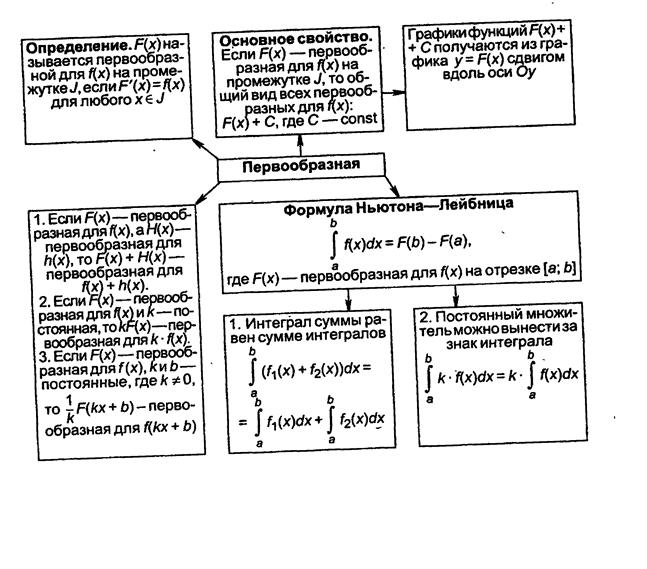
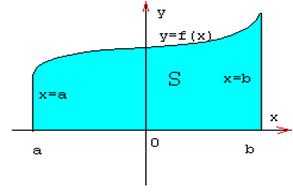
2. Фигура, изображённая на рисунке является криволинейной трапецией

Определение

Криволинейной трапецией называется фигура, ограниченная сверху графиком непрерывной функции y=f(x), снизу отрезком [a;b] оси Ох, а с боков отрезками прямых х=а, х=b

Площадь криволинейной трапеции можно вычислить с помощью определённого интеграла

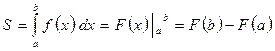
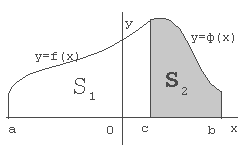Возможно такое расположение:

S = S₁+ S₂

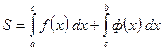
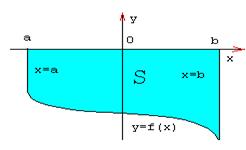
Возможен следующий случай, когда f(x) < 0 на [а,b]

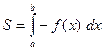
Возможно и такое расположение

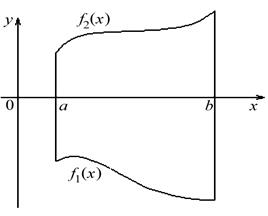S=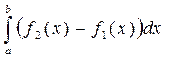

Задачи на вычисление площадей плоских фигур можно решать по следующему плану:

1) по условию задачи делают схематический чертёж;

2) представляют искомую фигуру как сумму или разность площадей криволинейных трапеций. Из условия задачи и чертежа определяют пределы интегрирования для каждой составляющей криволинейной трапеции.

3) записывают каждую функцию в виде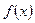

4) вычисляют площадь каждой криволинейной трапеции и искомой фигуры.

Задача

Найти площадь фигуры, ограниченной линиями.

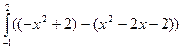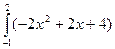S = dx = dx =

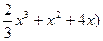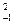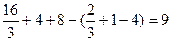= (- | =- (кв. ед.)

Литература:

1. Ш.А.Алимов «Алгебра и начала анализа» 10-11 кл. , стр. 293 – 298

2. Ш.А.Алимов «Алгебра и начала анализа» 10-11 кл. , стр. 300 – 304

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.