Хелпикс

Главная

Контакты

Случайная статья



Метод итераций для системы уравнений в Excel



 

Метод простой итерации даёт возможность получить последовательность приближённых значений, сходящуюся к точному решению системы.
Преобразуем систему (3.1) к нормальному виду:
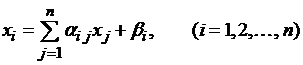. (3.2)
Правая часть системы (3.2) определяет отображение:
x=(x1, x2, ..., xn), преобразующее точку n-мерного метрического пространства в точку y=(y1, y2, ..., yn) того же пространства.
Выбрав начальную точку x0=(x01, x02, ..., x0n), можно построить итерационную последовательность точек n - мерного пространства: x0, x1=F(x0), ... , xn+1=F(xn)
При определённых условиях данная последовательность сходится.
Так, для исследования сходимости таких последовательностей используется принцип сжимающих отображений, который состоит в следующем.
Если F– сжимающее отображение, определённое в полном метрическом пространстве с метрикой ρ(x,y), то существует единственная неподвижная точка x*, такая, что x*=F(x*). При этом итерационная последовательность, {xn}, полученная с помощью отображения F с любым начальным членом х(0), сходится к x*.
Оценка расстояния между неподвижной точкой x* отображения F и приближением х(к) даётся формулами:
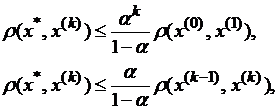(3.3)
где α – множитель, определяемый достаточными условиями сжимаемости отображения F.
Значение множителя α, определяется выбором метрики, в которой проверяется сходимость последовательности значений xi.

Рассмотрим достаточные условия сходимости итерационной последовательности {xn}.
Практически, для применения метода итерации систему линейных уравнений удобно "погрузить" в одну из трёх следующих метрик:
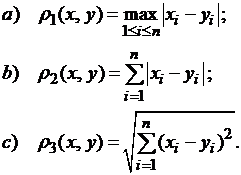(3.4)
Для того, чтобы отображение F, заданное в метрическом пространстве соотношениями (3.2), было сжимающим, достаточно выполнение одного из следующих условий:
а) в пространстве с метрикой ρ1: 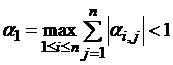, т. е. максимальная из сумм модулей коэффициентов в правой части системы (3.2), взятых по строкам, должна быть меньше единицы.
б) в пространстве с метрикой ρ2: 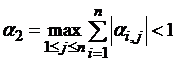, т. е. максимальная из сумм модулей коэффициентов в правой части системы (3.2), взятых по столбцам, должна быть меньше единицы.
в) в пространстве с метрикой ρ3: 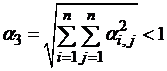, т. е. сумма квадратов при неизвестных в правой части системы (3.2) должна быть меньше единицы

ПРИМЕР. Вычислить два приближения методом простой итерации. Оценить погрешность второго приближения. В качестве начального приближения выбрать x0=(0; 0; 0).

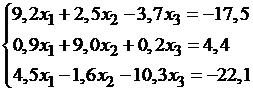
Так как диагональные элементы системы являются преобладающими, то приведем систему к нормальному виду:

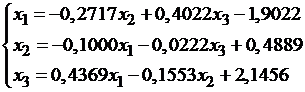
Последовательные приближения будем искать по формулам:

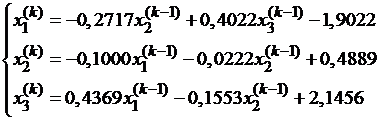
Получаем:
x1=(-1.9022; 0.4889; 2.1456), x2=(-1.1720; 0.6315; 1.2389).
Для оценки погрешности в метрике ρ1 вычисляем коэффициент μ
.
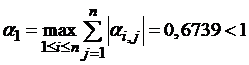Вычисляем погрешность: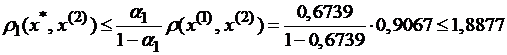

При большом числе неизвестных схема метода Гаусса, дающая точное решение, становится весьма сложной. В этом случае для решения СЛАУ иногда удобнее пользоваться методом простой итерации.

Метод итераций для системы уравнений в Excel

На листе Excel организуется таблица в три зоны: первая зона состоит из одного столбца (номер итерации), вторая зона определяет переменные x, третья зона под вычисления точности epsilon.
Во второй зоне по итерационной схеме организуется расчет переменных x (в примере для случая трех переменных):
Итерация №1:=$F$2/$B$2-C6*$C$2/$B$2-D6*$D$2/$B$2;=$F$3/$C$3-B6*$B$3/$C$3-D6*$D$3/$C$3;=$F$4/$D$4-B6*$B$4/$D$4-C6*$C$4/$D$4
Итерация №2:=$F$2/$B$2-C7*$C$2/$B$2-D7*$D$2/$B$2;=$F$3/$C$3-B7*$B$3/$C$3-D7*$D$3/$C$3;=$F$4/$D$4-B7*$B$4/$D$4-C7*$C$4/$D$4

Для вычисления точности epsilon.
Итерация №1:=ABS(B7)-ABS(B6);=ABS(C7)-ABS(C6);=ABS(D7)-ABS(D6)
Итерация №2:=ABS(B8)-ABS(B7);=ABS(C8)-ABS(C7);=ABS(D8)-ABS(D7)
Скачать шаблон решения.

ПРИМЕР. Методом итераций решить систему линейных алгебраических уравнений предварительно приведя ее к диагональному преобладанию.
Решение. Приведем матрицу к диагональному преобладанию.
Умножаем матрицы ATA.

ATA=
-12
-12
 

Умножаем матрицы ATb.

ATb=
-41
-88
 

Приведем к виду:
x1=7.25-1.5x3
x2=-0.8+0.24x3
x3=-3.67-0.5x1+0.5x2
Покажем вычисления на примере нескольких итераций.
N=1
x1=7.25 - 0 • 0 - 0 • (-1.5)=7.25
x2=-0.8 - 0 • 0 - 0 • 0.24=-0.8
x3=-3.67 - 0 • (-0.5) - 0 • 0.5=-3.67
N=2
x1=7.25 - (-0.8) • 0 - (-3.67) • (-1.5)=1.75
x2=-0.8 - 7.25 • 0 - (-3.67) • 0.24=0.0588
x3=-3.67 - 7.25 • (-0.5) - (-0.8) • 0.5=0.36
N=3
x1=7.25 - 0.0588 • 0 - 0.36 • (-1.5)=7.79
x2=-0.8 - 1.75 • 0 - 0.36 • 0.24=-0.89
x3=-3.67 - 1.75 • (-0.5) - 0.0588 • 0.5=-2.82
Остальные расчеты сведем в таблицу.

N x1 x2 x3 e1 e2 e3
     
7.25 -0.8 -3.67 7.25 0.8 3.67
1.75 0.0588 0.36 -5.5 -0.75 -3.31
7.79 -0.89 -2.82 6.04 0.83 2.46
3.02 -0.14 0.67 -4.77 -0.75 -2.15
8.26 -0.96 -2.09 5.24 0.82 1.41
4.12 -0.31 0.94 -4.14 -0.65 -1.14
8.67 -1.03 -1.45 4.55 0.71 0.51
5.07 -0.46 1.18 -3.59 -0.56 -0.27
9.02 -1.08 -0.9 3.95 0.62 -0.28
5.9 -0.59 1.38 -3.12 -0.49 0.49
9.33 -1.13 -0.42 3.42 0.54 -0.96
6.62 -0.71 1.56 -2.7 -0.42 1.14
9.59 -1.17 -0.00351 2.97 0.47 -1.56
7.24 -0.8 1.71 -2.35 -0.37 1.71
9.82 -1.21 0.36 2.58 0.4 -1.36
7.79 -0.89 1.85 -2.04 -0.32 1.49
10.02 -1.24 0.67 2.24 0.35 -1.18
8.26 -0.96 1.96 -1.77 -0.28 1.29

После N-ой итерации получаем: x1 = 7.5, x2 = -0.75, x3 = 0.25
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.