
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
МАТЕМАТИКА 1 курс
МАТЕМАТИКА 1 курс
Тест
1. Решить уравнение: SIN Х = 1
а) х =  + 2πn n ε z б) х = π + πn n ε z в) х = 0 г) х = 2πn n ε z
+ 2πn n ε z б) х = π + πn n ε z в) х = 0 г) х = 2πn n ε z
2. Производная функции у =( 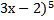 равна:
равна:
а) 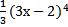 б) 15 *
б) 15 * 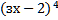 в) 3 *
в) 3 * 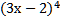 г) 10 * ( 3х – 2)
г) 10 * ( 3х – 2)
3. Объем конуса равен:
а) π r h б) π 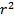 h в)
h в)  π
π 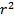 h г) 2π
h г) 2π 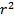 h
h
4. Вычислить интеграл: 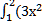 + 2 )dx
+ 2 )dx
а) 5 б) 8 в) 1 г) 9.
5. Подбрасывают две игральные кости, какова вероятность того, что произведение выпав -
ших очков будет кратно 6.
а) 0,9 б) 0,6 в) 0,3 г) 0,2
6. Вычислите: 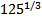 +
+ 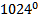 -
- 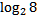 +
+ 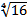
а) 0 б) 5 в) 1 г) 8
7. Производная сложной функции равна произведению производной промежуточной
функции на:
а) производную основной функции б) вторую производную функции
в) интеграл этой функции г) постоянную величину этой функции.
8. Решите неравенство: 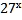 ≥
≥ 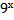 .
.
а) [ -1 ; +∞ ) б) ( 0 ; +∞) в) [ 0 ; + ∞ ) г) ( 1 ; + ∞).
9. Выражение 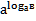 равно:
равно:
а) а б) с в) 1 г) в.
10. Уравнение, содержащее переменную под знаком логарифма, называется:
а) степенным б) логарифмическим в) показательным г) линейным.
11. Цилиндр и конус имеют одинаковые основания и высоту, если объем конуса равен 12 π ,
то объем цилиндра равен:
а) 24 π б) 16 π в) 36 π г) 64 π
12. Корень уравнения 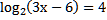 равен:
равен:
а) 5 б) 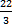 в) -7 г) нет корней
в) -7 г) нет корней
13. Решите систему уравнений: 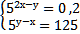
а) (-2; 4) б) (1; 3) в) (2; 5) г) (7; 9)
14. Вычислите: (1.4 – 3.5:1  ):2.4+3.4:2
):2.4+3.4:2 
а) 1 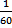 б)
б) 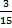 в) 0.5 г) -0.2
в) 0.5 г) -0.2
15. функция, заданная формулой: у=ах, где а>0, а ≠1 называется:
а) степенной б) показательной в) квадратичной г) линейной
16. Степенью числа а>0 с рациональным показателем p=  , где m – целое число, а n – натуральное (n>1) называется число:
, где m – целое число, а n – натуральное (n>1) называется число:
а) 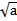 б)
б) 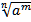 в) 1 г)
в) 1 г) 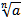
17. Вычислите  о
о
а) 1 б) 0 в) 0.5 г) -1
18. Упростите выражение: 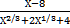
а) 1 б) 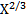 +2 в) Х-2 г)
+2 в) Х-2 г) 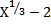
19. Число 4 представьте в виде суммы двух неотрицательных слагаемых так, чтобы произведение этих чисел было наибольшим.
а) 1+3 б) 2.5+1.5 в) 2+2 г) 0.5+3.5
20. Упростите выражение: 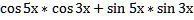
а) 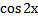 б)
б) 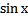 в)
в)  г)
г) 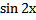
21. В правильной четырехугольной пирамиде сторона основания 8м , апофема 5м . Объем
пирамиды равен: а) 40 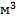 б) 56
б) 56 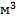 в) 60
в) 60 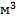 г) 64
г) 64 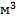 .
.
22. Первообразная функции f(x) = 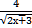
а) 0,5 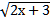 б) 2
б) 2 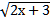 в) 4
в) 4 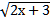 г)
г) 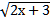
23. Найдите область определения функции: у = 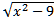
а) [3; +∞) б) (-∞; -3] в) [-3; 3] г) (-∞; -3] U [3; +∞)
24. Найдите сумму двадцати членов арифметической прогрессии, если первый её член равен 2, а седьмой равен 20.
а) 476 б) 608 в) 576 г) 610
25. Интегралом от а до b функции f(x) называется:
а) дифференциал этой функции б) первообразная этой функции
в) максимальное значение функции г) приращение первообразной F(x) этой функции.
26. Если скалярное произведение векторов равно, то векторы:
а) коллиниарны б) сонаправлены в) перпендикулярны
г) противоположно направленны
27. Даны координаты точек А (-4;1;-2) В (3;-6;7) С (2; 5; 8). Найдите скалярное произведение векторов 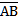 и
и 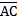
а) -95 б) 104 в) 112 г) 106
28. Найдите площадь фигуры, ограниченной линиями у = 4 - 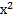 и у= 0
и у= 0
а) 10 б) 10  в) 11
в) 11  г) 12.
г) 12.
29. Материальная точка движется прямолинейно по закону S (t)= 4 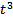 -
- 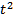 . Найдите ускорение этой точки в момент времени t = 2 с.
. Найдите ускорение этой точки в момент времени t = 2 с.
а) 30 б) 46 в) 48 г) 36.
30. Свежие грибы содержат по массе 90 % воды, а сухие – 12 % воды. Сколько получится сухих
грибов из 22 кг свежих грибов?
а) 3 кг б) 2,5 кг в) 2 кг г) 1,5 кг.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|