Классная работа. Предел функции на бесконечности

22.05.20. Классная работа. Предел функции на бесконечности

1. Изучение нового материала.

Вычисление предела функции на бесконечности осуществляется по тем же теоремам как и предел функции в точке.

Теорема 1 Для любого натурального показателя m и любого коэффициента k справедливо соотношение

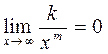, где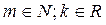

Теорема 2: предел суммы двух функций при х стремящемся к бесконечности равен сумме двух пределов

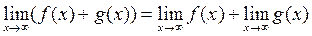
Теорема 3: предел произведения двух функций при х стремящемся к бесконечности равен произведению двух пределов

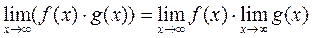
Теорема 4: предел частного двух функций при х стремящемся к бесконечности равен частному двух пределов, при условии что знаменатель не равен нулю:

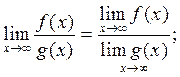если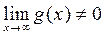

Теорема 5: постоянный множитель можно вынести за знак предела

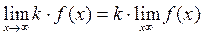
Основные формулы предела функции на бесконечности

1) 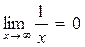2) 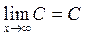, где С – любое число 3) 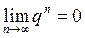, где |q|<1, q - число

Алгоритм нахождения предела функции на бесконечности

1) применить теоремы либо 2 либо 3 либо 4

2) применить теорему 1 или основные формулы

3) вычислить предел

4) Если нельзя применить теоремы 1-2-3- 4 и основные формулы, то нужно

каждый член числителя и знаменателя разделить на х в высшей степени для каждой дроби