
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Исследование процессов обработки древесины с использованием методов дробного факторного эксперимента
Практическая работа
Исследование процессов обработки древесины с использованием методов дробного факторного эксперимента
Цель: исследование процессов обработки древесины с использованием методов дробного факторного эксперимента.
Задача эксперимента: установить зависимость выходного параметра y
от влияющих факторов x1 – x5.
Варианты заданий на практическую работу №3 «Исследование процессов обработки древесины с использованием методов дробного факторного эксперимента» выбираются в соответствии с двумя последними цифрами зачетной книжки и приведены в табл. 15. Экспериментальные данные результатов многофакторных экспериментов (варианты заданий практической работы №3) приведены в табл. 20 настоящей работы.
Таблица 20 Экспериментальные данные результатов многофакторных
экспериментов
| Вариант 4 | |||||
| Определить зависимость водопоглащения ДСтП у, % от плотности х1, х2, х3, х4 и количества связующего в плите х5=12 %. | |||||
| Уровни факторов | Факторы | ||||
| х1, кг/м3 | х2, кг/м3 | х3, кг/м3 | х4, кг/м3 | х5, % связующе го | |
| Основной (нулевой) | 12,0 | ||||
| Нижний | 11,8 | ||||
| Верхний | 12,2 | ||||
| Интервал варьирования | 0,2 | ||||
| у изменяется от 65 до 30 %, рис. 21 | |||||
Проведем обработку экспериментальных данных многофакторного эксперимента, характеризующих зависимость предела прочности ДСтП при статическом изгибе y, МПа от продолжительности прессования x1 – x4, мин и давления прессования х5, МПа.
Цель: Определить зависимость водопоглощения ДСтП y,% от плотности методом дробного факторного эксперимента.
Решение:
При планировании опытов используем методику проведения дробного факторного эксперимента (ДФЭ) первого порядка с двухуровневым варьированием фактора. Воспользуемся ¼ реплики ПФЭ, т. е. ДФЭ типа 25-2, где два фактора заменены соответствующими произведениями остальных факторов (x4=x1∙x2; x5=x1∙x2∙x3).
Это позволит сократить число опытов до 23=8.
Уровни варьирования факторов представлены в табл. 21.
Таблица 21 Переменные факторы эксперимента и уровни варьирования
| Уровни факторов | Факторы | |||||
| x1, кг/м3 | x2, кг/м3 | x3, кг/м3 | x4, кг/м3 | x5, % связующие его | ||
| Основной (нулевой) | ||||||
| Нижний | 11,8 | |||||
| Верхний | 12,2 | |||||
| Интервал варьирования | 0,2 | |||||
Y изменяется от 65 до 30, рис.21
В табл. 22 приведены матрица планирования ДФЭ 25-2 и результаты экспериментов – значения выходной переменной, в нашем случае, – предел прочности при статическом изгибе у.
Для обработки результатов эксперимента используем методику, изложенную в главе 4.
1. Расчет построчных средних:
yj1 + yj 2 + ... + yjm
yj = m ,
где m – число повторных опытов (m=2). Результаты расчета представлены в табл. 22.
2. Определение построчных (выборочных) дисперсий:
| å |
(yji - yj)2
σ2j =
i=1 ;
m -1
| σ |
| = |
| = |
1 2 -1
22 + 22 = 8
σ 2 =
(66-62)2 + (58-62)2 = 42 + 42 = 32
2 2 -1
| σ |
| = |
| = |
3 2 -1
12 + 12 = 2
| σ |
| = |
4 2 -1
| σ |
| = |
5 2 -1
| σ |
| = |
6 2 -1
| σ |
| = |
7 2 -1
| σ |
| = |
8 2 -1
32 + 32 = 18
22 + 22 = 8
32 + 32 = 18
12 + 12 = 2
1,52 + 1,52 = 4,5
Сумма построчных (выборочных) дисперсий:
σ 2∑ = 8+32+2+18+8+18+2+4,5 = 92,5
Таблица 22
| Матрица ДФЭ 2^(5-2) с двумя параллельными опытами | |||||||||||||
| № | x0 | x1 | x2 | x3 | x4 | x5 | Построчная дисперсия | ||||||
| опыт 1 | опыт 2 | среднее | модель | ||||||||||
| -1 | -1 | -1 | 61,5 | ||||||||||
| -1 | -1 | -1 | |||||||||||
| -1 | -1 | 63,5 | |||||||||||
| -1 | -1 | ||||||||||||
| -1 | -1 | -1 | 63,5 | ||||||||||
| -1 | -1 | -1 | |||||||||||
3. Определение однородности дисперсий по критерию Кохрена:
Gэксп =
o 2 j max =
o 2 å
32 = 0,345946.
92,5
Далее по табл. П3 находим Ga,m1,m2.
Для a = 0,05; m1 = m – 1= 2 – 1= 1 и m2 = 8.
Значение G0,05, 1, 8 = 0,68. Поскольку Gэксп <Gтеор (0,34< 0,68), то дисперсии однородны.
4. Определение коэффициентов в уравнении регрессии:
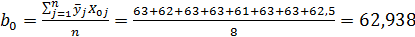
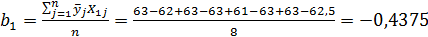
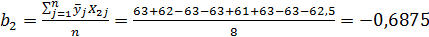
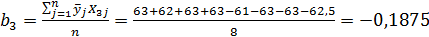
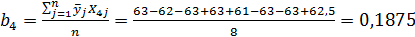
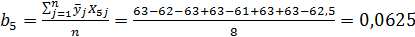
5.
| n |
ås 2 j
σ 2восп =
j =1 =
n
o 2 å =
n
96 = 11,5625
Дисперсия коэффициентов уравнения регрессии:
σ 2в =
o 2 восп =
| 0,75 |
12 = 0,75
8 × 2
σв =
o 2в =
= 0,87
Находим значение доверительного интервала для коэффициентов регрессии: ∆bj = ta,m ∙ σ в.
Здесь m1 = n(m–1) = 8(2–1) = 8, тогда теоретическое значение критерия Стьюдента t0,05, 8 = 2,31 (табл. П1), откуда ∆bj = 2,31∙0,87 = 2,0
Сопоставляем доверительный интервал ∆bj с абсолютными значениями коэффициентов модели b1, b2, b3, b4, b5 , принимаем b1 = – 0,25 и b2 = – 0,75. Уравнение будет иметь следующий вид:
ŷ = 62,938 – 0,437х1 – 0,187х2
Результаты расчета выходных параметров по уравнению полученной модели ŷj занесем в табл. 22.
6.
| n |
Проверка адекватности полученной модели. Предварительно определим дисперсию адекватности:
må( yj - yˆj)2
σ 2ад =
j =1
n - C
В нашем случае m = 2, n = 8, С = 3 – число значимых коэффициентов в уравнении регрессии. И в результате имеем:
σ2ад =2
ŷ1 =62,3125
ŷ2 =63,1875
ŷ3 =62,6875
ŷ4 = 63,5625
ŷ5 =62,3125
ŷ6 =63,5625
ŷ7 =62,6875
ŷ8 = 63,5625
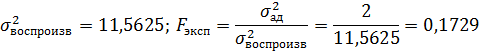
Теоретическое значение критерия Фишера Fa;m1;m2 при a = 0,05 можно определить по табл. П2; m1 = (n – C) = 8 – 3 = 5; m2 = n(m– 1) = 8(2 – 1) = 8
Значение F0,05, 5, 8 = 3,69. Поскольку Fэксп < Fтеор (0,1729<3,69), то модель адекватна.
Выводы по работе (пример 2, исследование процесса лущения березового шпона, рис. 17):
В ходе обработки экспериментальных данных мы использовали методику дробного факторного эксперимента первого порядка с двухуровневым варьированием фактора.
Были определены дисперсия 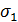 ...
... 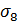 и обобщённая дисперсия
и обобщённая дисперсия 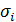 , построено уравнение регрессии, а также оценены: - однородность дисперсии в различных опытах по критерию Кохрена
, построено уравнение регрессии, а также оценены: - однородность дисперсии в различных опытах по критерию Кохрена 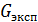 ; - коэффициенты ур-ния регрессии
; - коэффициенты ур-ния регрессии 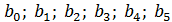 . А также были сделаны 2 проверки:
. А также были сделаны 2 проверки:
1) проверка значимости коэффициентов регрессии 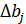
2) проверка адекватности полученного регрессионного уравнения по критерию Фишера 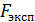
Кроме того, при планировании эксперимента методом ДФЭ мы выяснили, что можно значительно сократить число опытов, воспользовавшись свойством реплики, где 2 фактора заменены соответствующими произведениями остальных факторов ( 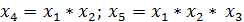 ), данная суть ДФЭ делает его применение в производственных условиях весьма эффективным.
), данная суть ДФЭ делает его применение в производственных условиях весьма эффективным.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|