ПОДОБИЕ ТЕЛ.

Дрозд Никита гр.№9КМ/13К

ПОДОБИЕ ТЕЛ.

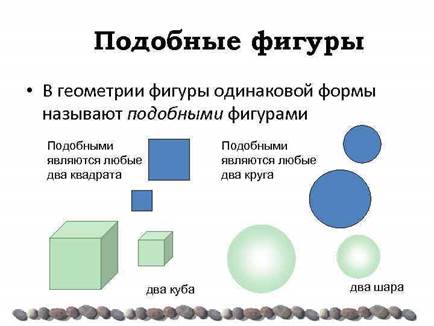
Два тела подобны, если одно из них может быть получено из другого путём увеличения ( или уменьшения ) всех его линейных размеров в одном и том же отношении. Автомобиль и его модель – подобные тела. Два тела ( фигуры ) зеркально подобны, если одно из них подобно зеркальному отражению другого. Например, картина и её фотонегатив зеркально подобны друг другу.

В подобных и зеркально подобных фигурах все соответственные углы ( линейные и двугранные ) равны.

В подобных телах многогранные и телесные углы равны; в зеркально подобных телах они зеркально равны. Если два тетраэдра ( две треугольные пирамиды ) имеют соответственно пропорциональные рёбра ( или соответственно подобные грани ), то они подобны или зеркально подобны. Например, если грани первой пирамиды вдвое больше, чем у второй, то высоты, апофемы, радиус описанного круга первой пирамиды также вдвое больше, чем у второй. Эта теорема не имеет места для многогранников с бо’льшим числом граней. Предположим, что мы соединили все рёбра куба в его вершинах посредством шарниров; тогда мы можем изменить форму этой фигуры, не растягивая её стержни, и получить из начального куба параллелепипед.

Две правильные призмы или пирамиды с одинаковым числом граней подобны, если радиусы их оснований пропорциональны их высотам. Два круглых цилиндра или конуса подобны, если радиусы их оснований пропорциональны их высотам.

Если два и более тел подобны, то площади всех соответствующих плоских и кривых поверхностей этих тел пропорциональны квадратам любых соответ-ствующих отрезков.

Если два и более тел подобны, то их объёмы, а также объёмы любых их соответ-ствующих частей, пропорциональны кубам любых соответствующих отрезков.