Четные и нечетные функции

Четные и нечетные функции

Из формулы (1) следует, что функция cos x такова, что при замене аргумента х на – х значение функции не меняется. Такие функции называют четными.

Функция f (x) называется четной,если для каждого х из области определения этой функции выполняется равенство

f (− x) = f (x)

График четной функции симметричен относительно оси ординат.

Из формулы (2) следует, что функция sin x при замене аргумента х на – х меняет знак. Такие функции называют нечетными.

Функция f (x) называется нечетной,если для каждого х из области определения этой функции выполняется равенство

f (− x) = − f (x)

График нечетной функции симметричен относительно начала координат.

Задача. Исследовать следующие функции на четность и нечетность:

1) f (x) = x sin x 2) f (x) = x cos x

1) Заменим х на – х, тогда f (− x) = −x sin (− x ) = (−x)(− sin x ) = x sin x,

Таким образом при замене х на – х, значение функции не меняется, следовательно функция x sin x - четная.

2) f (- x) = −x cos ( − х) = −х cos х = − f (x),

Таким образом при замене х на – х, значение функции изменилось, следовательно функция x cos x - нечетная.

Самостоятельно.

Исследовать функцию на четность и нечетность.

1) f (x) = x ² + 7 2) f (x) = −3 x ³

Вычислить sin 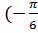) = − sin = − ,

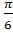cos (− ) = cos = .

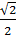Самостоятельно

1) cos (− ) sin 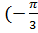) + tg ( − ),

2) cos (−π) + 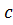tg ( − ) − sin 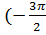) + 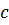tg ( − ).

Значения углов смотреть в таблице тема: «Тригонометрические функции».