
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Преподавателю (Маркарян Нана Степановна) писать на
Преподавателю (Маркарян Нана Степановна) писать на
email vstepmark@mail.ru
whatsapp +7 903 288 37 17
При отправлении заданий не забывайте писать свою фамилию, имя и номер группы обязательно!
Занятие №12
Движение материальной точки по окружности.
Вращательное движение твёрдого тела
При движении материальной точки по окружностинаправление вектора линейного ускорения не совпадает с направлением вектора линейной скорости. В любой точке траектории линейная скорость v тела направлена по касательной к окружности, а вектор ускорения a может быть разложен на два вектора: aк и aц (рис. 1), где aк – составляющая вектора ускорения a по касательной к траектории в данной точке, называемая касательным (тангенциальным) ускорением; aц – составляющая вектора ускорения a по нормали (радиусу) к касательной к траектории в данной точке, называемая центростремительным (нормальным) ускорением:
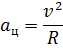
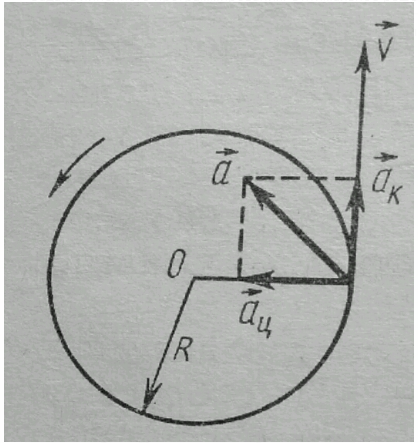
Рис. 1
Из рисунка видно, что
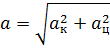
При равномерном движении по окружности (aк = 0) a = aц и направлено по радиусу к центру окружности. В этом случае:
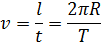
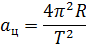
где l – длина окружности; T – период вращения (время одного полного оборота); R – радиус окружности.
Вращательное движение твёрдого тела характеризуют следующие величины: 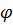 – угловое перемещение (угол поворота произвольного радиуса от начального положения);
– угловое перемещение (угол поворота произвольного радиуса от начального положения); 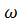 – угловая скорость;
– угловая скорость;  –частота вращения; T – период вращения. Величины
–частота вращения; T – период вращения. Величины 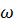 ,
, 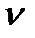 и T связаны между собой соотношением:
и T связаны между собой соотношением:
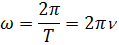
При равномерном вращении тела уравнение движения:
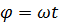
При равнопеременном вращении тела (равноускоренном или равнозамедленном) уравнение его движения, а также формула зависимости угловой скорости от времени движения имеют вид:
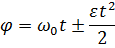
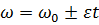
где 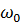 – начальная угловая скорость;
– начальная угловая скорость; 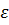 – угловое ускорение.
– угловое ускорение.
В этих формулах выбирают знак «+» для равноускоренного вращения, знак «–» – для равнозамедленного.
Угловые величины 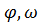 и
и 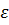 связаны с соответствующими линейными величинами l, v и a следующими соотношениями:
связаны с соответствующими линейными величинами l, v и a следующими соотношениями:
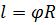 ;
; 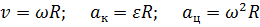
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|