
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Векторы в пространстве. Вариант 2
Векторы в пространстве
Вариант 2
ABCDA1B1C1D1 - параллелепипед. Укажите вектор, равный сумме

| |
В правильной треугольной призме ABCA1B1C1 сторона основания равна 1, точка Е – середина А1С1.
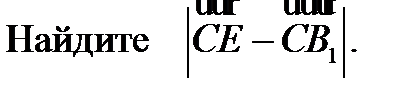 1)
1) 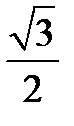 2) 2) 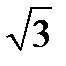 3) 3) 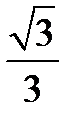 4) 4) 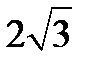
| |
ABCDA1B1C1D1 – параллелепипед. A1С пересекает В1D в точке М.
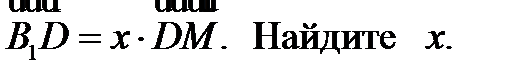 1) 3 2) -2 3) -1 4) 2
1) 3 2) -2 3) -1 4) 2
| |
| Выберите верные высказывания: 1) Длины равных векторов равны. 2) Векторы, лежащие на двух прямых, параллельных одной плоскости, коллинеарны. 3) Любые три вектора некомпланарны. 4) Векторы, лежащие на боковых ребрах призмы, коллинеарны. Ответ: ______ | |

| |
Диагонали куба ABCDA1B1C1D1 пересекаются в точке О.
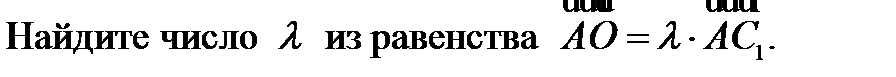 Ответ: ______
Ответ: ______
| |
SO – высота правильной четырехугольной пирамиды SABCD.
 Ответ: ______
Ответ: ______
| |
В кубе ABCDA1B1C1D1 назовите вектор, равный сумме
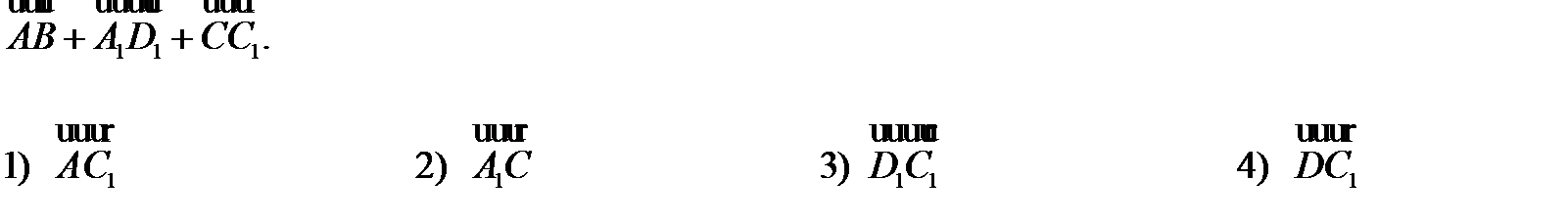
| |
Дан тетраэдр DABC. Назовите ребро тетраэдра, изображающее вектор 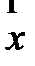 , если векторы , если векторы 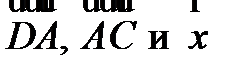 компланарны, но никакие два из них не коллинеарны.
1) AC 2) DC 3) DA 4) AB компланарны, но никакие два из них не коллинеарны.
1) AC 2) DC 3) DA 4) AB
| |
В пирамиде PАВСD основанием служит параллелограмм АВСD;
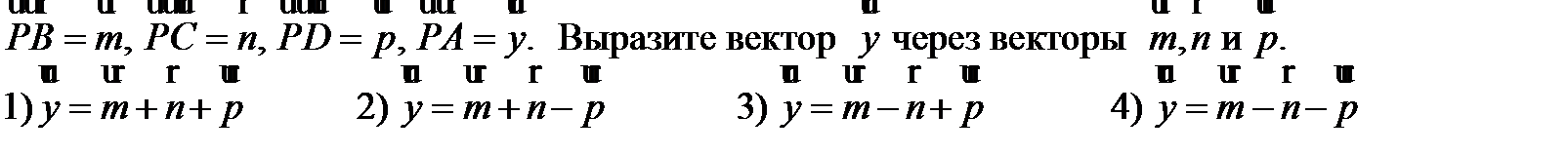
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|