Главная
Контакты
Случайная статья
Задания для контрольных работ по дисциплине «Математика» Задания для контрольных работ по дисциплине «Математика»
Таблица для выбора заданий
№ варианта
Номер задания
Контрольная работа № 1
Контрольная работа № 2
Примечание:
Контрольная работа № 1 «Матрицы. Система линейных уравнений»
1. Пусть даны две матрицы и . Найдите матрицу и ее определитель .
1.
,
2.
,
3.
,
4.
,
5.
,
7.
,
8.
,
9.
,
10.
,
11.
6.
,
12.
2. Решить систему линейных уравнений методом Крамера, Гаусса и матричным способом.
1. 2. 3. 4.
5. 6. 7. 8.
9. 10. 11. 12.
Контрольная работа № 2 «Векторная алгебра»
1. Даны вектора 1 ; y1 ), 2 ; y2 ), 3 ; y3 ). Найдите координаты векторов и длину:
1)
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
2. Расстояние от точки В, лежащей на оси …, до точки А (х; у) равно…. Найдите координаты точки В.
1. на оси оу, А(2;1), 3
2. на оси ох, А(3;4), 6
3. на оси оу, А(-1;2), 4
4. на оси ох, А(2;-3), 5
5. на оси оу, А(-8;1), 10
6. на оси ох, А(-4;-3), 7
7. на оси оу, А(7;-1), 11
8. на оси ох, А(4;-2), 8
9. на оси оу, А(2;-3), 12
10. на оси ох, А(2; -7), 9
11. на оси оу, А(2;3), 12
12. на оси ох, А(-2; 7), 10
3. Точка А(x1 ; y1 ), В(x2 ; y2 ), С(x3 ; y3 ) служат вершинами параллелограмма, причем А и С - противоположные вершины. Найдите четвертую вершину D.
1. А(0;8) В(-4;-5) С(-8;-2)
2. А(6;5) В(-6;0) С(-10;3)
3. А(10;-1) В(-2;-6) С(-6;-3)
4. А(7;1) В(-5;-4) С(-9;-1)
5. А(1;3) В(9;-1) С(2;-3)
6. А(-5;5) В(1;3) С(3;7)
7. А(2;-2) В(3;-5) С(5;1)
8. А(-2;0) В(8;8) С(6;-2)
9. А(0;2) В(0;4) С(2;4)
10. А(-3;3) В(5;-1) С(5;-5)
11. А(0;-2) В(0;-4) С(-2;-4)
12. А(3;-3) В(-5;1) С(-5;5)
4. Треугольник задан вершинами: А(х1 , у1 ), В(х2 , у2 ), С(х3 , у3 ). Найдите: 1) уравнение прямой ВN, параллельной стороне АС; 2) уравнение медианы СD; 3) уравнение высоты АЕ; 4) угол В.
1. А(8;0) В(-5;-4) С(-2;-8)
2. А(5;6) В(0;-6) С(3;-10)
3. А(-1;10) В(-6;-2) С(-3;-6)
4. А(1;7) В(-4;-5) С(-1;-9)
5. А(3;1) В(-1;9) С(-3;2)
6. А(5;-5) В(3;1) С(7;3)
7. А(-2;2) В(-5;3) С(1;5)
8. А(0;-2) В(8;8) С(-2;6)
9. А(2;0) В(4;0) С(4;2)
10. А(3;-3) В(-1;5) С(-5;5)
11. А(-2;0) В(-4;0) С(-4;-2)
12. А(-3;3) В(1;-5) С(5;-5)
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.


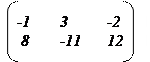 1.
1. 
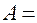
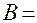
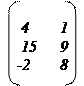
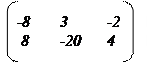 2.
2.
 3.
3.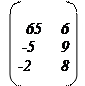
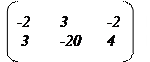 4.
4.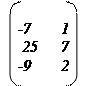
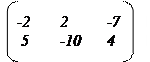 5.
5.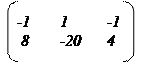
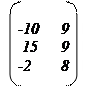 7.
7.
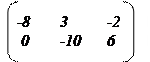 8.
8.
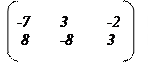 9.
9.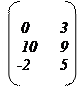
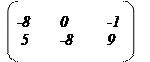 10.
10.
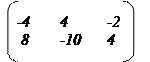 11.
11.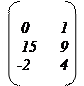
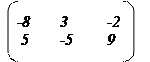 6.
6.
 12.
12.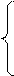
 1.
1. 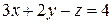 2.
2. 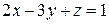 3.
3. 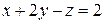 4.
4. 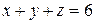
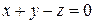
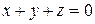
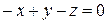
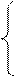
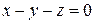
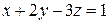
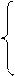
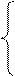 5.
5. 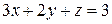 6.
6. 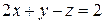 7.
7. 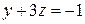 8.
8. 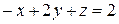
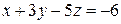
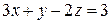
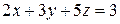
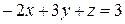
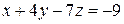
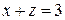
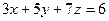
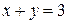
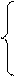
 9.
9. 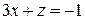 10.
10. 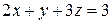 11.
11. 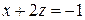 12.
12. 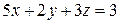
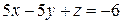
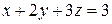
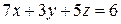
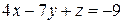
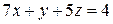
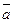 =(x1; y1),
=(x1; y1), 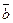 =(x2; y2),
=(x2; y2), 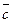 =(x3; y3). Найдите координаты векторов и длину:
=(x3; y3). Найдите координаты векторов и длину: