Единый государственный экзамен по МАТЕМАТИКЕ

Единый государственный экзамен по МАТЕМАТИКЕ

Вариант 106

Инструкция по выполнению работы

Экзаменационная работа состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 8 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 4 задания повышенного уровня сложности с кратким ответом и 7 заданий повышенного и высокого уровней сложности с развёрнутым ответом.

На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).

Ответы к заданиям 1–12 записываются по приведённому ниже образцу в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите их в бланк ответов № 1.

При выполнении заданий 13–19 требуется записать полное решение и ответ в бланке ответов № 2.

Все бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается использование гелевой, капиллярной или перьевой ручек.

При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.

Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.

Желаем успеха!

Справочные материалы

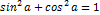
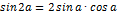
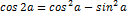
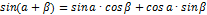
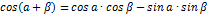
Часть 1

Ответом к заданиям 1–12 является целое число или конечная десятичная дробь. Запишите число в поле ответа в тексте работы, затем перенесите его в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания, начиная с первой клеточки. Каждую цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений писать не нужно.

В школе 500 учеников, из них 30% — ученики начальной школы. Среди учеников средней и старшей школы 10% изучают французский язык. Сколько учеников в школе изучает французский язык, если в начальной школе французский язык не изучается?

Ответ: ________________

На рисунке показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей температурами воздуха 18 декабря. Ответ дайте в градусах Цельсия.

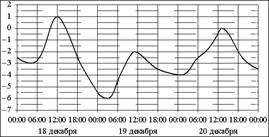
Ответ: ________________

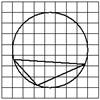На клетчатой бумаге с размером клетки 1×1изображён треугольник. Найдите радиус описанной около него окружности.

        Ответ: ________________

Комната освещается светильником с двумя лампами. Вероятность перегорания одной лампы в течении года равна 0,3. Найдите вероятность того, что в течение года перегорит только одна лампа.

   Ответ: ________________

Найдите корень уравнения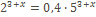

   Ответ: ________________

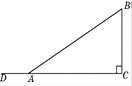
В треугольнике ABC угол C равен 90°, косинус угла В=0,6. Найдите косинус внешнего угла при вершине А.

Ответ: ________________

На рисунке изображён график функции y=f′(x) — производной функции f(x), определённой на интервале (2; 13). Найдите точку максимума функции f(x).

Ответ: ________________

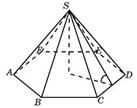
Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45°. Найдите объем пирамиды.

Ответ: ________________

Часть 2

Найдите значение выражения: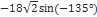

Ответ: ________________

Деталью некоторого прибора является вращающаяся катушка. Она состоит из трех однородных цилиндров: центрального массой m=8 кг и радиуса R=10 см, и двух боковых c массами M=1 кг и c радиусами R+h. При этом момент инерции катушки относительно оси вращения, выражаемый в 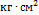, дается формулой 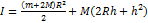. При каком максимальном значении h момент инерции катушки не превышает предельного значения 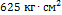? Ответ выразите в сантиметрах.

Ответ: ________________

Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.

Ответ: ________________

Найдите точку максимума функции

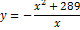
Ответ: _______________

Не забудьте перенести все ответы в БЛАНК ОТВЕТОВ № 1.

Для записи решений и ответов на задания 13-19 используйте БЛАНК ОТВЕТОВ № 2. Запишите сначала номер выполняемого задания (13, 14 и т.д.), а затем полное обоснованное решение и ответ. Ответы записывайте четко и разборчиво.

а) Решите уравнение

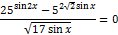
б) Найдите все корни этого уравнения, принадлежащие отрезку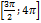

Дан цилиндр, в котором проведены диаметры оснований. AB – диаметр верхнего основания, CD - диаметр нижнего, причем отрезки AB и CD не лежат на параллельных прямых.

а) Докажите, что у пирамиды ABCD противоположные ребра равны.

б) Найдите высоту цилиндра, если AC=7, AD=6, а радиус основания цилиндра равен 2,5.

Решите неравенство:

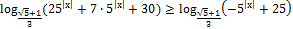
Прямая, проходящая через вершину B прямоугольника ABCD перпендикулярно диагонали AC, пересекает сторону AD в точке M, равноудалённой от вершин B и D.

а) Докажите, что ∠ABM=∠DBС=30°.

б) Найдите расстояние от центра прямоугольника до прямой CM, если BC=9.

15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:

— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r— целое число;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг (в млн. руб.)		0,6	0,4	0,3	0,2	0,1

Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.

Найдите значения a, при каждом из которых система уравнений

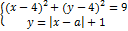
имеет ровно три решения.

а) Существует ли конечная арифметическая прогрессия, состоящая из пяти натуральных чисел, такая, что сумма наибольшего и наименьшего членов этой прогрессии равна 99?

б) Конечная арифметическая прогрессия состоит из шести натуральных чисел. Сумма наибольшего и наименьшего членов этой прогрессии равна 9. Найдите все числа, из которых состоит эта прогрессия.

в) Среднее арифметическое членов конечной арифметической прогрессии, состоящей из натуральных чисел, равно 6,5. Какое наибольшее количество членов может быть в этой прогрессии?