ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 19. Краткие теоретические сведения. Содержание работы. Вариант 1

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 19

Тема:Решение задач на правила логического вывода

Краткие теоретические сведения

Классическое исчисление высказываний задаётся следующими аксиомами и правилами вывода:

Аксиомы:

1. A → (B → A),

2. (A → (B → C)) → ((A → B) → (A → C)),

3. A ∧ B → A,

4. A ∧ B → B,

5. A → (B → A ∧ B),

6. A → A ∨ B,

7. B → A ∨ B,

8. (A → C) → ((B → C) → (A ∨ B → C)),

9. (A → B) → ((A → B) → A),

10. A → A.

Правило вывода (modus ponens, MP)

Определение. Выводом в исчислении высказываний (или просто выводом) называется конечная последовательность формул, каждая из которых является аксиомой или получается из некоторых предыдущих формул по правилу вывода.

Таблица истинности для логических операций:

A	B	A ∧ B	A ∨ B	A → B	~ A	A → B	B → A	A ↔ B
И	И	И	И	И	Л	И	И	И
И	Л	Л	И	Л	Л	Л	И	Л
Л	И	Л	И	И	И	И	Л	Л
Л	Л	Л	Л	И	И	И	И	И

Пример 1. Следующая последовательность формул является выводом:

P → Q ∨ P

Q → Q ∨ P

(P → Q ∨ P) → ((Q → Q ∨ P) → (P ∨ Q → Q ∨ P))

(Q → Q ∨ P) → (P ∨ Q → Q ∨ P) (MP)

P ∨ Q → Q ∨ P (MP).

Пример 2. Проверьте валидность аргумента, если

Посылка. 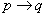Посылка.

Вывод.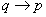

Решение. Составляем таблицу истинности:


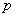
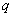
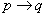
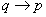
И	И	Л	И	И	И
И	Л	Л	Л	Л	И
Л	И	И	И	И	Л
Л	Л	И	И	И	И

В третьей строке обе посылки истинны, а вывод - ложный. Следовательно, аргумент не валидный.

Содержание работы

Вариант 1

Задание 1.Проверьте валидность аргумента и составьте таблицу истинности, если

a) Посылка. a ˅ b Посылка. b→a

Вывод. a→b

б) Посылка. a → b Посылка. ͂ b˅ ͂ a

Вывод. a↔b

Вариант 2

Задание 1.Проверьте валидность аргумента и составьте таблицу истинности, если

a) Посылка. a ˄ b Посылка. b↔a

Вывод. a→b

б) Посылка. a ˄ ͂ b Посылка. b→a

Вывод. a↔b