ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 20. Краткие теоретические сведения. Содержание работы. Вариант 1

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 20

Тема:Решение задач на множества

Краткие теоретические сведения

Основные операции над множествами

Объединениеммножеств A и B называется множество A∪B={x|(x∈A)∨(x∈B)}.

Например, если 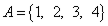, , 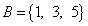, 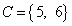то , , .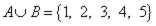

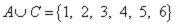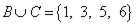Пересечениеммножеств и называется множество A∩B={x|(x∈A)∧(x∈B)}.

Например, если 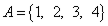, , 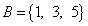, 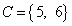то , , .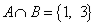

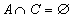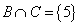Множество, состоящее из всех элементов множества A, не принадлежащих множеству B, называется разностью множеств A и B: A∖B={x|(x∈A)∧(x∉B)}.

Например, если 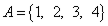, , 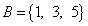, 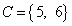то , , , .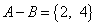

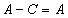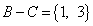
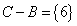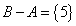Если A⊂B, то B∖A называют дополнением множества A до множества B:A_B′.

Если, в частности, A− подмножество некоторого универсального множества U, то разность U∖A обозначается символом 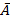или A′ и называется дополнением множества A (до множества U).

Из определения дополнения множества следуют равенства A∪A′=U;A∩A′=∅,(A′)′=A.

Симметрической разностью множеств A и B называют множество AΔB, состоящее из тех и только тех элементов, которые принадлежат только одному из множеств A или B, то есть

AΔB=(A∖B)∪(B∖A).

Для любых подмножеств A и B множества U справедливы следующие равенства, которые называют законами двойственности или законами де Моргана:

(A∪B)′=A′∩B′; (A∩B)′=A′∪B′.

Содержание работы

Вариант 1

Задание 1. Записать множества A∪B, С∪B, A∪С, если А={1,2,3,6}, B={3,6,8,9}, С={0,2,3,9}.

Задание 2. Записать множество A∩B, С∩B, A∩С , если А={4,5,8,9}, B={0,4,8}, С={2,8,9}.

Задание 3. Записать множество A∖B, С∖B, A∖С, если А={1,3,8,9}, B={0,2,3,8}, С={0,4,9}.

Вариант 2

Задание 1. Записать множества A∪B, С∪B, A∪С, если А={4,5,6,7}, B={5,6,8,9}, С={4,6,9}.

Задание 2. Записать множество A∩B, С∩B, A∩С , если А={5,8,9}, B={5,6,8}, С={0,5,6}.

Задание 3. Записать множество A∖B, С∖B, A∖С, если А={0,1,3,5}, B={0,3,6,8}, С={5,8,9}.