
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 39. Краткие теоретические сведения. Формулы решений простейших тригонометрических уравнений. Содержание работы
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 39
Тема:Решение тригонометрических уравнений сводящихся к квадратным
Краткие теоретические сведения
Отличительные признаки уравнений, сводящихся к квадратным:
1. В уравнении присутствуют тригонометрические функции от одного аргумента или они легко сводятся к одному аргументу.
2. В уравнении присутствует только одна тригонометрическая функция или все функции можно свести к одной.
Пример. Решить уравнение: 2sin2x+sinx-1=0.
Решение: Замена: sinx=y
2у2+у-1=0.
D=1-4∙2∙(-1) = 9>0, то уравнение имеет 2 различных корня.
у1 = -1; у2 = 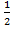 .
.
Совершим обратную замену:
sinx = -1 sinx = 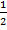
х = - 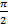 +2
+2 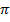 n, n
n, n 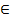 Z; х = (-1)n
Z; х = (-1)n  +
+ 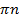 , n
, n 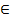 Z.
Z.
Ответ:- 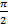 +2
+2 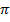 n, n
n, n 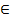 Z; (-1)n
Z; (-1)n  +
+ 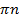 , n
, n 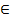 Z.
Z.
Итак, чтобы решить уравнение такого вида, нужно:
1. Ввести новую переменную у.
2. Совершить замену простейшего тригонометрического уравнения на у.
3. Решить получившееся квадратное уравнение.
4. Совершить обратную замену.
5. Решить простейшие тригонометрические уравнения.
6. Записать ответ.
Формулы решений простейших тригонометрических уравнений
7. 
8. 
9. 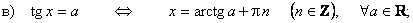
10. 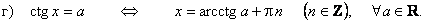
Содержание работы
| Вариант 1 | Вариант 2 |
| Решить уравнения: | |
| а) 2sin2x+3sinx+1=0 б) 6cos2x-5cosx+1=0 в) 8tg2x-6tgx-5=0 г) ctg2x-2ctgx+1=0 | а) 3sin2x-5sinx-2=0 б) cos 2x+5 cos x+6=0 в) tg2x+tgx-2=0 г) ctg2x-5ctgx+4=0 |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|