
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ПРАКТИЧЕСКАЯ РАБОТА «Координаты и векторы»
ПРАКТИЧЕСКАЯ РАБОТА «Координаты и векторы»
ЦЕЛЬ РАБОТЫ:научиться находить координаты середины отрезка; координаты вектора по координатам начала и конца; выполнять действия над векторами, заданными своими координатами;
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1.Повторить материал в учебнике.
2. Ответить на контрольные вопросы:
-Связь координат вектора с координатами начала и конца.
-Вычисление длины вектора.
-Формула расстояния между двумя точками.
-Скалярное произведение векторов.
-Формула для нахождения координат середины отрезка.
- Условие коллинеарности двух векторов
Содержание практической работы
| I вариант | II вариант |
1. Точка А – середина отрезка МN.
Найти координаты точки А и длину отрезка МN, если N (5; 2; -3);
М (3; -2; 1)
(1 балл)
2. Точки А (-2; -4; 1) и В (-5; -6; -1) и вершины параллелограмма АВСD, точка О (1; 3; 2) – точка пересечения диагоналей.
Найти координаты вершин С и D.
(2 балла)
3.Даны точки А (-2; 1; 3), В(3; -2; -1),
С (-3; 4; 2).
Найти:
1) Координаты векторов 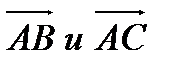 (0,5 балла)
2) Модули векторов
(0,5 балла)
2) Модули векторов 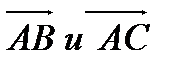 (0,5 балла)
3) Координаты векторов
(0,5 балла)
3) Координаты векторов 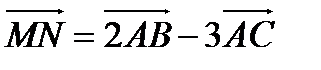 (1 балл)
4.Даны векторы
(1 балл)
4.Даны векторы 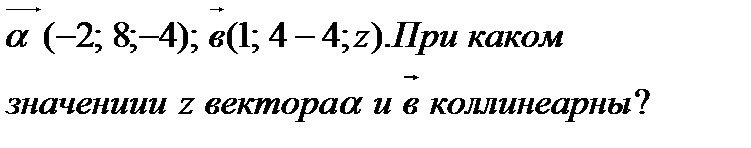 (2 балла)
5. Вычислить скалярное произведение векторов
(2 балла)
5. Вычислить скалярное произведение векторов 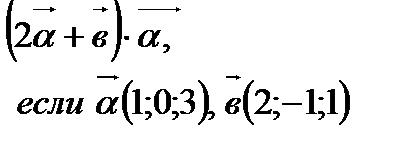 (3балла)
(3балла)
| 1. Точка Р – середина отрезка АВ.
Найти координаты точки А и длину отрезка АВ, если В (-6; 5; -3);
М (3; -2; 1)
(1 балл)
2. Точки А (2; -4; 1), В (-6; 2; 3) и D (-4; 0; -1) вершины параллелограмма АВСD, точка О (1; 3; 2) – точка пересечения диагоналей.
Найти координаты вершин С и D.
(2 балла)
3.Даны точки А (-2; 1; 3), В(3; -2; -1),
С (-3; 4; 2).
Найти:
1) Координаты векторов 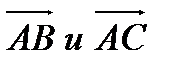 (0,5 балла)
2) Модули векторов
(0,5 балла)
2) Модули векторов 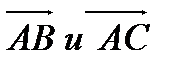 (0,5 балла)
3) Координаты векторов
(0,5 балла)
3) Координаты векторов 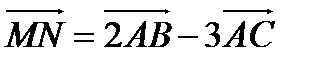 (1 балл)
4.Даны векторы
(1 балл)
4.Даны векторы 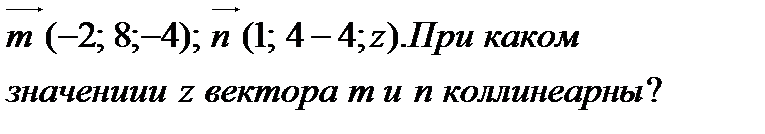 (2 балла)
5. Вычислить скалярное произведение векторов
(2 балла)
5. Вычислить скалярное произведение векторов 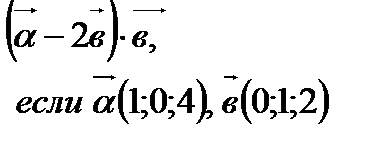 (3балла)
(3балла)
|
3.Изучить условие заданий для практической работы и критерии оценки.
4.Оформить отчет о работе.
| Время выполнения | 80 минут |
| Критерии оценивания | Отметка "5" -10 баллов Отметка "4" 7--9 баллов Отметка "3" 4-6 баллов Отметка "2" –менее 4 баллов |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|