
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача 2. Задача 3. Задача 4. Задача 5. Задача 6. Задача 7. Задача 8. Задача 9. Задача 10
Задача 2
Дано:
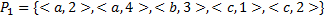
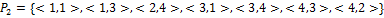 .
.
Решение:
Матрицы заданных бинарных отношений:
[  ]=
]= 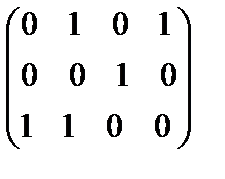 , [
, [  ]=
]= 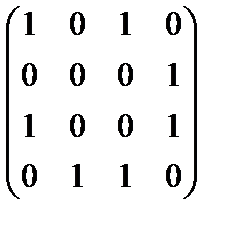 .
.
Матрица [ 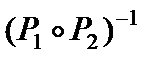 ] :
] :
[ 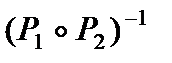 ]=
]= 
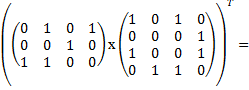

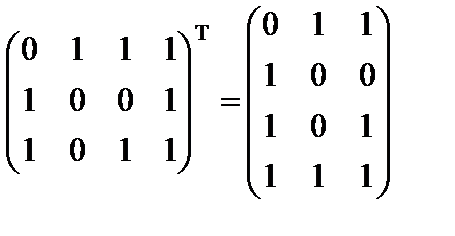 .
.
Отношение Р2 – нерефлексивно, так как на главной диагонали ее матрицы имеются нулевые элементы.
Отношение Р2 – симметрично, так как ее матрица симметрична относительно главной диагонали.
Отношение Р2 не является антисимметричным, так как
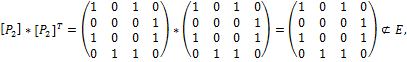
где Е - единичная матрица,  операция поэлементного умножения матриц
операция поэлементного умножения матриц
Отношение Р2 не является транзитивным, так как
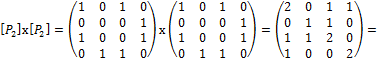
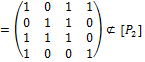
Задача 3
Дано: 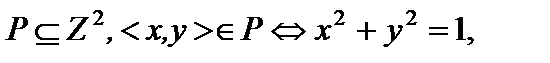
где Z – множество целых чисел.
Решение:
Область определения Р: 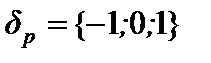 .
.
Область значений Р: 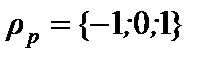 .
.
Отношение Р не является рефлексивным, так 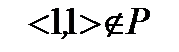 .
.
Отношение Р симметрично, так как 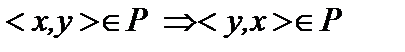 . Отношение Р не является антисимметричным, так как
. Отношение Р не является антисимметричным, так как 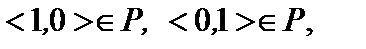 но
но 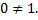
Задача 4
Дано: 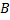 =
= 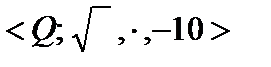 , где
, где  – множество рациональных чисел.
– множество рациональных чисел.
Решение:
Структура В не является алгеброй, так как операция 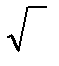 не замкнута на множестве
не замкнута на множестве  .
.
Задача 5
Дано:
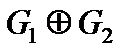
|
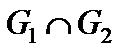
|
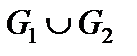
|
Матрица смежности А графа 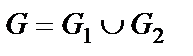 :
:
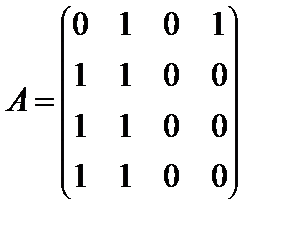 .
.
Граф G с указанием всех его дуг:
|
|
|
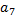
|
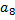
|
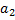
|
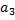
|
Матрица инцидентности D, соответствующая этому графу:
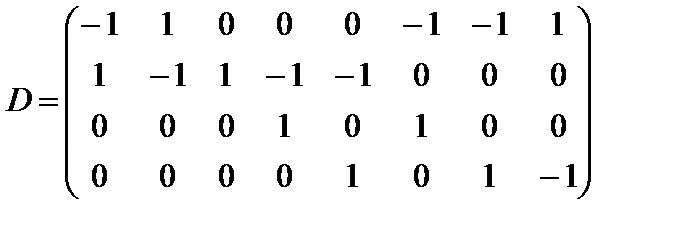
 .
.
Матрица сильных компонент связности S графа G: 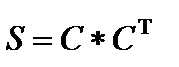 , где С-матрица достижимости графа G .
, где С-матрица достижимости графа G .
Для определения матрицы достижимости С графа G составляется матрица В и в ней ненулевые элементы заменяются цифрой 1.
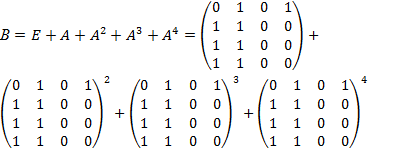 =
= 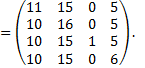
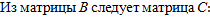
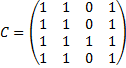 .
.
Матрица сильных компонент связности S графа G:
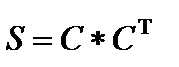
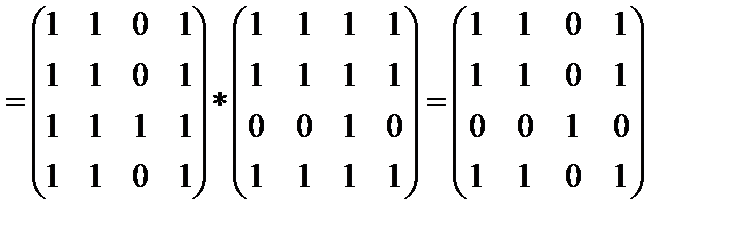 -.
-.
Матрица маршрутов длины 2:
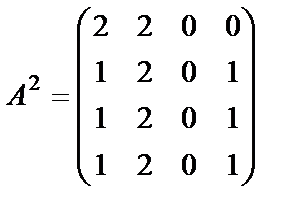 .
.
Отсюда следует, что граф содержит 4 маршрута длины 2, исходящие из вершины 1. Из них 2 маршрута циклические, а остальные заканчиваются на 2-ой вершине.
Найденные маршруты:
(1;2;1); (1;2;2); (1;4;1); (1;4;2).
Задача 6
Решение:
Граф содержит n вершин, m ребер и с компонент связности. Остов графа получается удалением из графа n – m+c=12-8+1=5 ребер, указанных на графе пунктирными линиями:
| a |
| в |
| c |
| d |
| e |
| f |
| g |
| h |
| i |
| l |
| m |
| k |
а b c d e f g h i k l m
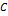 =
= 
 .
.
Матрица фундаментальных разрезов заданного графа:
а b c d e f g h i k l m
 =
= 
 .
.
Граф не является эйлеровым, так как степени не всех его вершин четные.
Граф планарный, так как ребра b и е можно изобразить без пересечения с другими ребрами в виде:
Задача 7
Дано: 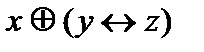 =
= 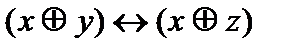
Решение:
Таблица истинности формулы 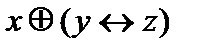
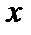
| 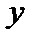
| 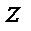
| 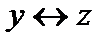
| 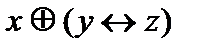
|
Таблица истинности формулы 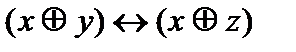
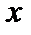
| 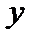
| 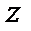
| 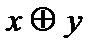
| 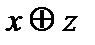
| 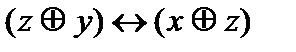
|
Формулы не эквивалентны, так как их таблицы истинности различаются.
Задача 8
Дано: 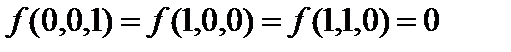 .
.
Решение:
1. Метод Квайна.
Таблица истинности заданной функции
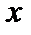
| 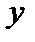
| 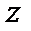
| 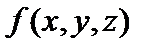
|
| 0 | |||
Из таблицы истинности следует, что СДНФ функции имеет вид:
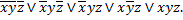 Далее путем преобразования формулы СДНФ на основе выполнения в два этапа все возможных операций неполного склеивания, а затем элементарного поглощения следует формула сокращенной ДНФ в виде:
Далее путем преобразования формулы СДНФ на основе выполнения в два этапа все возможных операций неполного склеивания, а затем элементарного поглощения следует формула сокращенной ДНФ в виде:
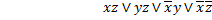 .
.
Нахождение тупиковых и минимальных ДНФ функции с помощью таблицы Квайна
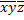
| 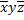
| 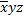
| 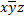
| 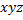
| |
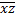
| * | * | |||
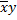
| * | * | |||
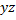
| * | * | |||
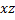
| * | * |
Из таблицы Квайна следуют варианты формул, минимальных ДНФ:
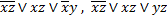 .
.
2. Метод карты Карно:
Сокращенная ДНФ получается путем покрытия всех «единичных» ячеек прямоугольниками, включающими 2к таких ячеек (к-целое число. Каждому прямоугольнику соответствует некоторая импликанта функции.
В случае покрытия четырьмя прямоугольниками следует сокращенная ДНФ, состоящая из четырех импликант:
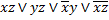
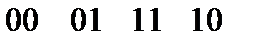
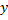
|
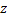
|
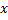
|
Покрытие минимальным количеством прямоугольников обеспечивает получение минимальных ДНФ.
Варианты минимальных ДНФ:
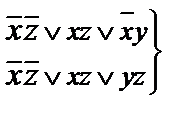
Задача 9
Задана система из двух функций:
J= 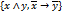
Функции заданной системы:
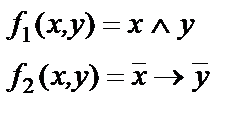
Определение принадлежности функций к классам Поста:
1) 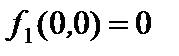 , поэтому функция
, поэтому функция 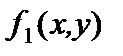 сохраняет ноль,
сохраняет ноль, 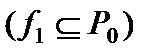 ;
;
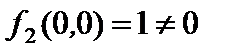 , поэтому функция
, поэтому функция 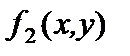 не сохраняет ноль,
не сохраняет ноль, 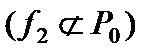 .
.
2) 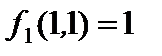 , поэтому функция
, поэтому функция 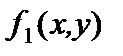 сохраняет единицу,;
сохраняет единицу,; 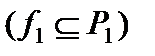 ;
;
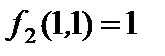 , поэтому функция
, поэтому функция 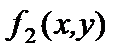 сохраняет единицу,
сохраняет единицу, 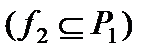 .
.
3) 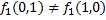 , поэтому функция
, поэтому функция 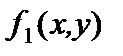 несамодвойственная ,
несамодвойственная , 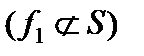 ;
;
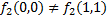 , поэтому функция
, поэтому функция 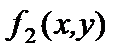 несамодвойственная,
несамодвойственная, 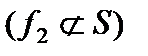 .
.
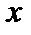
| 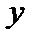
| 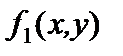
|
4)
Так как из условия 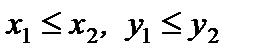 следует, что
следует, что 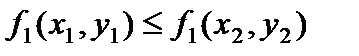 то функция
то функция 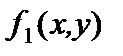 монотонная
монотонная 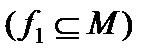 .
.
Так как 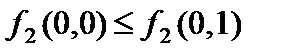 , то функция
, то функция 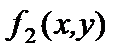 немонотонная
немонотонная 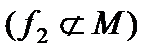 .
.
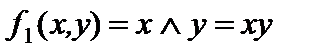 5). Полином Жегалкина для функции
5). Полином Жегалкина для функции 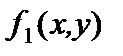 :
:
Функция 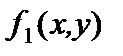 нелинейная, так как ее полином Жегалкина нелинейный.
нелинейная, так как ее полином Жегалкина нелинейный.
Полином Жегалкина для функции 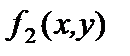 :
: 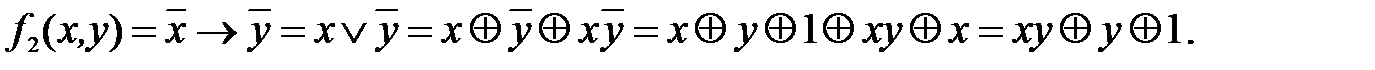 Функция
Функция 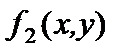 нелинейная, так как ее полином Жегалкина нелинейный.
нелинейная, так как ее полином Жегалкина нелинейный.
Таблица принадлежности функции к классам Поста
| Функция | Классы поста | ||||
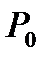
| 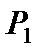
| 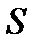
| 
| 
| |
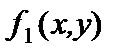
| да | да | нет | да | нет |
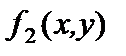
| нет | да | нет | нет | нет |
Система заданных функций не является полной, так как не для каждого из классов в системе Jнайдется функция, не принадлежащая этому классу.
Задача 10
Дано: Количество разрядов числа равно 5. Любые две соседние цифры различны.
Решение:
Пятизначному числу с цифрами х1, х2, х3, х4, х5можно сопоставить строку (х1, х2, х3, х4, х5). При этом выбор цифры х1возможен 9 способами; если х1 выбрана, то для выбора х2 имеется тоже 9 возможностей (х2может быть любой из цифр 0,1,2,…,9, отличной от х1) ; после выбора х , х2для х3 имеется снова 9 возможностей и т.д. Применяя правило произведения, находим, что искомое количество чисел есть 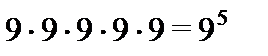 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|