Хелпикс

Главная

Контакты

Случайная статья



Теоретический материал. Задания для самостоятельного решения



 

Практическая работа по теме: «Решение тригонометрических уравнений методом замены переменной»

Цель: повторить метод замены переменной при решении тригонометрических уравнений.

Теоретический материал

Опр.: Уравнение называется тригонометрическим, если неизвестная величина входит в него как аргумент тригонометрической функции.

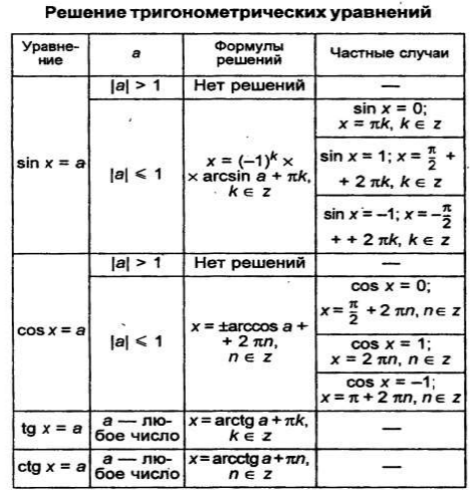
К этим уравнениям сводятся все другие. Для большинства таких уравнений требуется применение различных формул и преобразование тригонометрических выражений.

 

Пример 1:  3sin2 x -6sin x +3 = 0 . Вводят новую

переменную sin x= t, получаем квадратное уравнение:

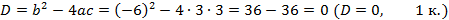
Получили корень уравнения, возвращаемся в замену:

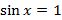 (частный случай)

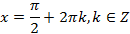
Ответ: 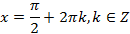Пример 2:

Рассмотрим уравнение 2 cos2 x + 5 sin x = 5.

Преобразуем его, применив основное тригонометрическое тождество:

 2(1 − sin2 x) + 5 sin x = 5,

2 sin2 x − 5 sin x + 3 = 0.

Заменяя sin x на t, приходим к квадратному уравнению: 2t 2 − 5t + 3 = 0.

Решая его, получим: t1 = , t2 = 1.

Теперь вспоминаем, что мы обозначили за t.

Первый корень приводит нас к уравнению sin x = . Оно не имеет решений, поскольку .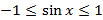

Второй корень даёт простейшее уравнение sin x = 1.

Решаем его: x = π 2 + 2πk, k ∈ Z. Это и есть ответ.

Задания для самостоятельного решения

Вариант I

Решите следующие тригонометрические уравнения методом замены переменной:

 

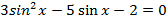
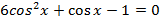
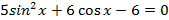
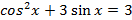
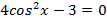
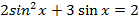
Вариант II

Решите следующие тригонометрические уравнения методом замены переменной:

 

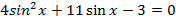
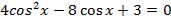
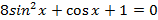
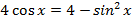
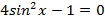
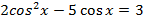
Выбор варианта индивидуальный.
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.