
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая работа № 21. Ход работы
Практическая работа № 21
Тема: «Производная и её применение».
Цели:
· повторить формулы и правила нахождения производной функции,
· физический и геометрический смысл производной,
· применение производной к исследованию функции.
План выполнения практической работы
Выполнить самостоятельную работу.
Ход работы
Вариант 1
1. Найдите значение производной функции 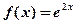 в точке
в точке 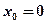 .
.
2. Материальная точка движется по закону х(t)=- t3 +6 t2 +5 t ( х – в метрах, t – в секундах). Определите скорость точки в момент, когда ее ускорение равно нулю.
3. Количество электричества, протекающее через проводник, начиная с момента t=0, по t=5 задаётся формулой q(t)=2t2+t+3. Найдите, в какой момент времени сила тока достигнет наименьшего значения.
4. На рисунке изображен график производной функции, определенной на интервале (-5;3). Найдите точки, в которых функция принимает наименьшее значение.
5. Найдите наибольшее значение функции y=x3+2x2+x+3 на отрезке [-4;-1].
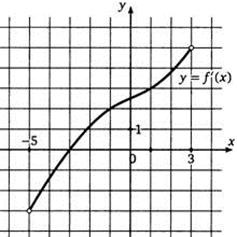
6. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
 |
Вариант 2
1. Найдите значение производной функции 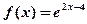 в точке
в точке 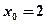 .
.
2. Материальная точка движется по закону х(t)= t3 -3 t2 +4 t ( х – в метрах, t – в секундах). Определите скорость точки в момент, когда ее ускорение равно нулю.
3. Количество электричества, протекающее через проводник, начиная с момента t=0, по t=10 задаётся формулой q(t)=3t2+t+2. Найдите, в какой момент времени сила тока достигнет наибольшего значения.
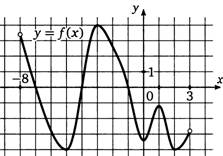
4. На рисунке изображен график производной функции, определенной на интервале (-8;3). В какой точке отрезка [-3;-1] функция принимает наибольшее значение.
5. Найдите наименьшее значение функции y=x3-3x2+2 на отрезке [1;4].
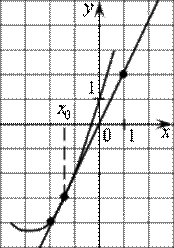
6. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
 |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|