Хелпикс

Главная

Контакты

Случайная статья



Практическая работа 7. Вариант 1



  Практическая работа 7

Тема: Решение задач с использованием численного интегрирования и дифференцирования

 

Цель: оценить погрешности точного и приближенного значения интеграла по формулам прямоугольников, трапеций и формуле Симпсона; уметь находить производную в точке с помощью интерполяционной формулы Ньютона. 

 

Вариант 1

 

Задания:

1.Исходные данные: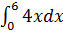

1) Вычислить определенный интеграл точно по формуле Ньютона-Лейбница.

2) Вычислить определенный интеграл приближенно по формуле прямоугольников.

3) Вычислить определенный интеграл приближенно по формуле трапеций.

4) Вычислить определенный интеграл приближенно по формуле парабол (Симпсона).

5) Выполнить оценку погрешности по каждой формуле.

 

2.Функция у=f(x)  задана в виде таблицы.

хi
yi 4,9 5,5 5,9

а=0,1

Найдите значение 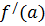 с точностью до сотых.

 

Ход работы

Практическая работа 7

Тема: Решение задач с использованием численного интегрирования и дифференцирования

 

Цель: оценить погрешности точного и приближенного значения интеграла по формулам прямоугольников, трапеций и формуле Симпсона; уметь находить производную в точке с помощью интерполяционной формулы Ньютона.  

 

Вариант 2

 

Задания:

1.Исходные данные: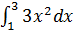

1) Вычислить определенный интеграл точно по формуле Ньютона-Лейбница.

2) Вычислить определенный интеграл приближенно по формуле прямоугольников.

3) Вычислить определенный интеграл приближенно по формуле трапеций.

4) Вычислить определенный интеграл приближенно по формуле парабол (Симпсона).

5) Выполнить оценку погрешности по каждой формуле.

 

2.Функция у=f(x)  задана в виде таблицы.

хi
yi 2,7 3,2 4,0

а=0,1

Найдите значение 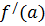 с точностью до сотых.

 

Ход работы

 
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.