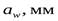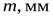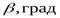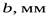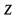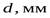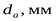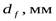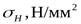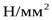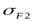- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическое задание №29 Проектный расчет закрытых цилиндрических передач
Практическое задание №29 Проектный расчет закрытых цилиндрических передач
1.Определяем главный параметр – межосевое расстояние 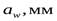 :
:
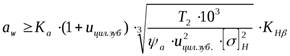 ,
,
где 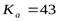 (для косозубых передач) – вспомогательный коэффициент,
(для косозубых передач) – вспомогательный коэффициент,
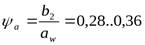 (для шестерни в нестандартных цилиндрических
(для шестерни в нестандартных цилиндрических
редукторах) – коэффициент ширины венца колеса, для расчета принимем 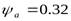 ,
,
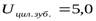 - передаточное число редуктора,
- передаточное число редуктора,
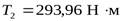 - вращающий момент на тихоходном валу,
- вращающий момент на тихоходном валу,
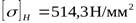 - допускаемое контактное напряжение,
- допускаемое контактное напряжение,
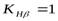 (для прирабатывающихся зубьев) – коэффициент неравномерности нагрузки по длине зуба.
(для прирабатывающихся зубьев) – коэффициент неравномерности нагрузки по длине зуба.

Округлив 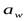 до стандартного значения, получаем
до стандартного значения, получаем 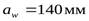 .
.
- Определяем модуль зацепления
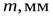 :
:
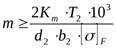 ,
,
где 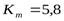 (для косозубых передач) – вспомогательный коэффициент,
(для косозубых передач) – вспомогательный коэффициент,
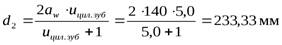 - делительный диаметр колеса,
- делительный диаметр колеса,
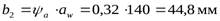 - ширина венца колеса,
- ширина венца колеса,
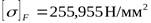 - допускаемое напряжение изгиба материала колеса,
- допускаемое напряжение изгиба материала колеса,
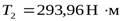 - вращающий момент на тихоходном валу.
- вращающий момент на тихоходном валу.
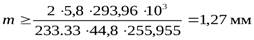 .
.
Округлив значение модуля зацепления 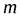 в большую сторону до стандартного значения, в целях обеспечения угла наклона зубьев
в большую сторону до стандартного значения, в целях обеспечения угла наклона зубьев  принимаем
принимаем 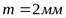 .
.
Тогда угол наклона зубьев для косозубой передачи будет равен:
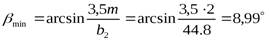 .
.
- Определяем суммарное число зубьев шестерни и колеса:
 .
.
Округлив 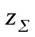 в меньшую сторону до целого числа, получаем значение суммарного числа зубьев
в меньшую сторону до целого числа, получаем значение суммарного числа зубьев 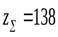 .
.
- Уточним действительную величину угла наклона зубьев для косозубых передач:
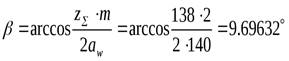 .
.
- Определяем число зубьев шестерни:
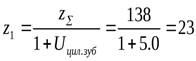 .
.
Округлив 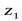 до ближайшего целого числа, получаем значение числа зубьев шестерни
до ближайшего целого числа, получаем значение числа зубьев шестерни 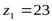 . Из условия уменьшения шума и отсутствия подрезания зубьев рекомендуется
. Из условия уменьшения шума и отсутствия подрезания зубьев рекомендуется 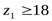 , при найденном значении
, при найденном значении 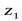 это условие выполняется.
это условие выполняется.
- Определяем число зубьев колеса:
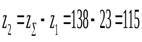 .
.
- Находим фактическое передаточное число:
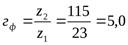 .
.
Проверяем фактического передаточного числа от заданного 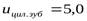 :
:
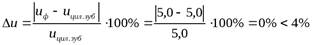 .
.
Норма передаточного числа выполняется.
- Определяем фактическое межосевое расстояние:
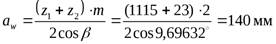
- Находим фактические основные геометрические параметры шестерни:
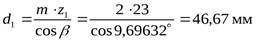 - делительный диаметр,
- делительный диаметр,
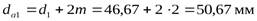 - диаметр вершин зубьев,
- диаметр вершин зубьев,
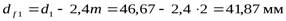 - диаметр впадин зубьев,
- диаметр впадин зубьев,
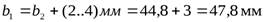 - ширина венца, округлив до целого стандартного значения по ряду Ra40, получаем значение
- ширина венца, округлив до целого стандартного значения по ряду Ra40, получаем значение 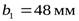 .
.
- Находим фактические основные геометрические параметры колеса:
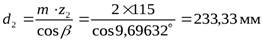 - делительный диаметр,
- делительный диаметр,
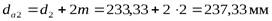 - диаметр вершин зубьев,
- диаметр вершин зубьев,
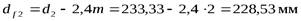 - диаметр впадин зубьев,
- диаметр впадин зубьев,
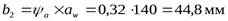 - ширина венца, округлив до целого стандартного значения по ряду Ra40, получаем значение
- ширина венца, округлив до целого стандартного значения по ряду Ra40, получаем значение 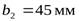 .
.
4.3. Силы в зацеплении передачи редуктора
Исходные данные: 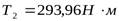 ,
, 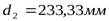 ,
, 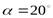 ,
, 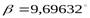 .
.
Окружная сила 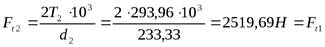 ,
,
радиальная сила  ,
,
осевая сила 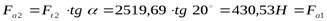 .
.
Схема сил в зацеплении:
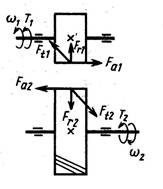
4.4. Проверочный расчет закрытой цилиндрической зубчатой передачи
4.4.1.Проверка прочности передачи на выносливость
- Проверим межосевое расстояние:
Полученное при проектном расчете межосевое расстояние 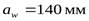 , найдем значение
, найдем значение 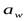 через делительные диаметры шестерни
через делительные диаметры шестерни 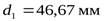 и колеса
и колеса 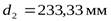 :
:
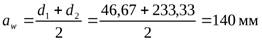 .
.
Проверка сошлась, расчет выполнен верно.
- Проверим пригодность заготовок колес.
Условие пригодности заготовок имеет вид: 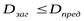 ,
, 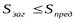 , где
, где 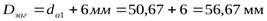 - диаметр заготовки шестерни.
- диаметр заготовки шестерни.
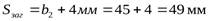 - толщина диска заготовки колеса
- толщина диска заготовки колеса
Предельные значения размеров заготовки: диаметр шестерни 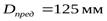 , толщина обода или диска колеса
, толщина обода или диска колеса 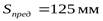 .
.
В результате получаем 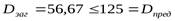 и
и  .
.
Проверка сходится, следовательно, заготовки колес пригодны.
- Проверим контактные напряжения (методику см. в учебном пособии А.Е. Шейнблит «Курсовое проектирование деталей машин», стр. 64-67):
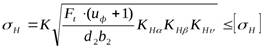 ,
,
где 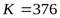 (для косозубых передач) – вспомогательный коэффициент,
(для косозубых передач) – вспомогательный коэффициент,
 - окружная сила в зацеплении (
- окружная сила в зацеплении ( 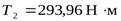 - вращающий момент на тихоходном валу редуктора,
- вращающий момент на тихоходном валу редуктора, 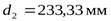 - делительный диаметр колеса):
- делительный диаметр колеса):
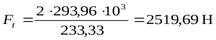 ,
,
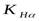 - коэффициент, учитывающий распределение нагрузки между зубьями, определяется по графику в зависимости от окружной скорости колес
- коэффициент, учитывающий распределение нагрузки между зубьями, определяется по графику в зависимости от окружной скорости колес 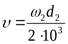 (
( 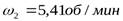 – угловая скорость на тихоходном валу редуктора):
– угловая скорость на тихоходном валу редуктора): 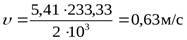 .
.
Для нахождения 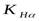 принимаем значение окружной скорости
принимаем значение окружной скорости 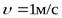 , тогда
, тогда 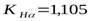 .
.
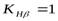 (для прирабатывающихся зубьев) – коэффициент неравномерности нагрузки по длине зуба,
(для прирабатывающихся зубьев) – коэффициент неравномерности нагрузки по длине зуба,
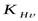 - коэффициент динамичности нагрузки, зависящий от окружной скорости колес и степени точности. Так как зубчатая передача косозубая цилиндрическая и окружная скорость
- коэффициент динамичности нагрузки, зависящий от окружной скорости колес и степени точности. Так как зубчатая передача косозубая цилиндрическая и окружная скорость 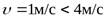 меньше, то степень точности 9. Следовательно,
меньше, то степень точности 9. Следовательно, 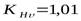 .
.
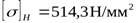 - допускаемое контактное напряжение.
- допускаемое контактное напряжение.
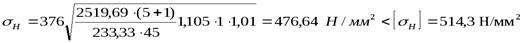 .
.
Найдем недогрузку передачи:
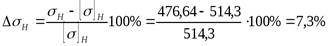 .
.
Так как допускается недогрузка  не более 10%, то условие будем считать выполненным.
не более 10%, то условие будем считать выполненным.
- Проверим напряжения изгиба зубьев шестерни
 и колеса
и колеса 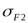 :
:
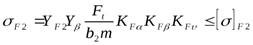
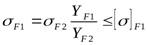 .
.
 - модуль зацепления,
- модуль зацепления,  - ширина зубчатого венца колеса,
- ширина зубчатого венца колеса,
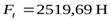 - окружная сила в зацеплении,
- окружная сила в зацеплении,
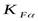 - коэффициент, учитывающий распределение нагрузки между зубьями, зависящий от степени точности передачи. Так как степень точности 9, то
- коэффициент, учитывающий распределение нагрузки между зубьями, зависящий от степени точности передачи. Так как степень точности 9, то 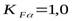 .
.
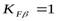 (для прирабатывающихся зубьев) – коэффициент неравномерности нагрузки по длине зуба,
(для прирабатывающихся зубьев) – коэффициент неравномерности нагрузки по длине зуба,
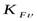 - коэффициент динамичности нагрузки, зависящий от окружной скорости колес и степени точности. Так как зубчатая передача косозубая цилиндрическая и окружная скорость
- коэффициент динамичности нагрузки, зависящий от окружной скорости колес и степени точности. Так как зубчатая передача косозубая цилиндрическая и окружная скорость 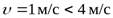 , степень точности 9. Следовательно,
, степень точности 9. Следовательно, 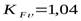 .
.
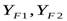 - коэффициенты формы зуба шестерни и колеса, зависящие от эквивалентного числа зубьев шестерни
- коэффициенты формы зуба шестерни и колеса, зависящие от эквивалентного числа зубьев шестерни 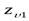 и колеса
и колеса 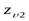 :
:
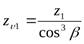 (
( 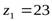 - число зубьев шестерни,
- число зубьев шестерни, 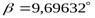 - угол наклона зубьев), тогда
- угол наклона зубьев), тогда 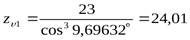 ,
,
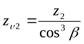 (
( 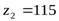 - число зубьев шестерни,
- число зубьев шестерни, 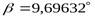 - угол наклона зубьев), тогда
- угол наклона зубьев), тогда 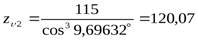 ,
,
По значениям 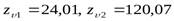 интерполированием (А.Е. Шейнблит «Курсовое проектирование деталей машин», таблица 4.4, стр.67) получаем
интерполированием (А.Е. Шейнблит «Курсовое проектирование деталей машин», таблица 4.4, стр.67) получаем 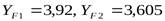 .
.
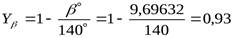 - коэффициент, учитывающий наклон зуба,
- коэффициент, учитывающий наклон зуба,
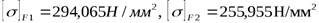 - допускаемые напряжения изгиба шестерни и колеса.
- допускаемые напряжения изгиба шестерни и колеса.
В результате получаем:
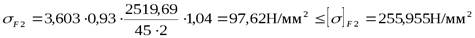
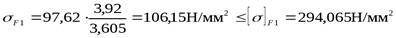 .
.
При проверочном расчете 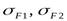 получились значительно меньше допускаемых значений, это допустимо, так как нагрузочная способность большинства зубчатых передач ограничивается контактной прочностью, следовательно, условие прочности выполнено.
получились значительно меньше допускаемых значений, это допустимо, так как нагрузочная способность большинства зубчатых передач ограничивается контактной прочностью, следовательно, условие прочности выполнено.
Следовательно, проектный расчет закрытой цилиндрической зубчатой передачи выполнен верно.
| Проектный расчет | |||||
| Параметр | Значение | ||||
| Шестерни (с индексом 1) | Колеса (с индексом 2) | ||||
| Межосевое расстояние | |||||
| Модуль зацепления | |||||
| Угол наклона зубьев | 9,69632 | ||||
| Ширина зубчатого венца | |||||
| Число зубьев | |||||
| Диаметр делительной окружности | 46,67 | 233,33 | |||
| Диаметр окружности вершин | 50,67 | 237,33 | |||
| Диаметр окружности впадин | 41,87 | 228,53 | |||
| Проверочный расчет | |||||
| Параметр | Допускаемые значения | Расчетные значения | |||
| Контактные напряжения | 514,3 | 476,64 | |||
| Напряжения изгиба
| шестерни | 294,065 | 97,62 | ||
| колеса | 255,955 | 106,15 | |||
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|