
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Подготовка к итоговой контрольной работе в группе № 17 (разбор заданий, подобных предложенным в итоговой контрольной работе))
Подготовка к итоговой контрольной работе в группе № 17 (разбор заданий, подобных предложенным в итоговой контрольной работе))
1. Вычислить: 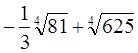
Решение. 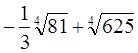 = -
= -  ∙3 + 5= -1+5=4. Ответ : 4
∙3 + 5= -1+5=4. Ответ : 4
2. Вычислить: 25-2 ∙ 510 : 1252
Решение. 25-2 ∙ 510 : 1252 =(52)-2 ∙ 510 :(53) 2= 5-4∙ 510 : 56 = 5-4 +10 – 6 =
= 50 = 1 Ответ : 1
(Используем свойства степеней: (am ) n = am n ; am ∙ an = am+n ; am : an =am-n)
3. Вычислить: log4 64
(Логарифмом числа b по основанию a называется показатель степени, в которую надо возвести число a, чтобы получить число b; log a b = c, ac = b)
Решение. log4 64 = 3, так как 43 = 64.
Ответ: 3
4. Вычислить: а) 2sin 22o30' cos22o30' = sin 450=√2/2 (Использовалась формула синуса двойного угла:
2sinα ∙ cosα = sin2α)
5. . Решить иррациональное уравнение: 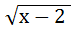 = 6
= 6
Решение. 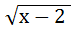 = 6, возведём обе части уравнения в квадрат (чтобы «избавиться» от квадратного корня);
= 6, возведём обе части уравнения в квадрат (чтобы «избавиться» от квадратного корня);
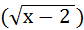 2 = 62;
2 = 62;
x – 2 = 36;
x = 36 +2;
x = 38.
Проверка при x = 38. 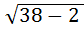 = 6
= 6
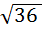 = 6 (верно).
= 6 (верно).
Ответ: 38.
6. Решить показательное уравнение: 32х + 1 = 27.
Решение. Представим правую часть уравнения в виде степени с основанием 3;
32х + 1 = 33; если равны степени и равны их основания, то равны и показатели этих степеней. Значит,
2x + 1 = 3;
2x = 3 – 1;
2x = 2;
x = 1.
Ответ: 1.
7).Решить логарифмическое уравнение log 3 ( 2x – 3) = 2
По определению логарифма 2x – 3= 32
2x – 3= 9
2x = 9 + 3
2x = 12
х = 12:2
х = 6.
Ответ: 6
8).Решить тригонометрическое уравнение 2sin x = 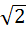
sin x = 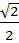
х = (-1)n arcsin 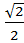 + π n, n
+ π n, n 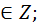
х = (-1)n 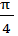 + π n, n
+ π n, n 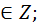
Ответ: (-1)n 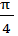 + π n, n
+ π n, n 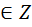 .
.
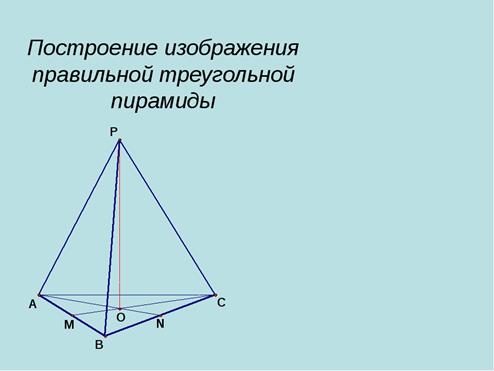
9.Задача. Основанием пирамиды РABC является правильный треугольник ABC со стороной 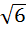 м. Высота пирамиды РО равна
м. Высота пирамиды РО равна 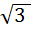 м. Найти объем пирамиды.
м. Найти объем пирамиды.
V =  S осн h (формула для вычисления объёма пирамиды)
S осн h (формула для вычисления объёма пирамиды)
S осн = S( 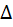 ABC) =
ABC) =  a2
a2 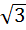 (формула для вычисления площади правильного треугольника).
(формула для вычисления площади правильного треугольника).
Значит, V =  S осн h =
S осн h = 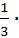
 a2
a2 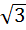 h (*)
h (*)
По условию задачи a = 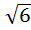 , высота h = РО =
, высота h = РО = 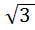 . Подставим в формулу(*)
. Подставим в формулу(*)
V= 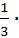

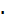 (
( 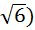 2
2 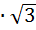
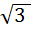 =
= 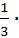

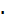 6
6 
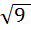 =
= 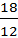 = 1,5 (м3).
= 1,5 (м3).
Ответ: 1,5 м3.
10).Задача. Найти площадь поверхности шара, если его диаметр равен 4 дм.
Решение:
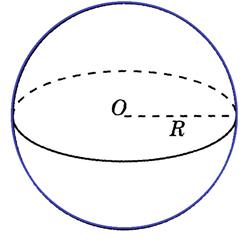
площадь поверхности шара (сферы) находим по формуле S = 4 π R2. Радиус шара равен половине диаметра, значит, R = 4 : 2 = 2 (дм).
S = 4 π R2 = 4 π ∙ 22 = 4∙π∙4 = 16 π (дм2).
Ответ: 16 π дм2.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|