Расчет ресурса оборудования по времени наступления постепенного отказа.

Стр 1 из 2Следующая ⇒

Федеральное государственное бюджетное учреждение

высшего образования

Нижегородский государственный

технический университет им. Р.Е. Алексеева

Кафедра

«Теоретическая и прикладная механика»

Отчет

по лабораторной работе №3

по дисциплине

«Диагностика технических систем»

тема

«Назначение ремонтов оборудования»

Вариант – 23

Выполнил

студент группы 14-СК

Головкина А.И.

Проверил

Запорожцев А.В.

Нижний Новгород

Цель работы:выбрать оборудование, которое требует проведения ремонта по нормативному сроку с учетом возможности параметрического отказа.

Исходные данные:

-Распределение наработки до отказа - нормальное;

-Вероятность, при которой назначают нормативный ремонт, Рн = 0,9;

-Число оборудования, находящееся в эксплуатации, Nоб = 20;

-Модель износа - линейная;

-Допустимое значение износа Хдоп = 10;

-Число объектов N=292;

-Среднее значение для формирования наработки M_t=51,73;

-Стандартное отклонение наработки S_t=9,51;

-Время начала планового периода T_п=21;

-Среднее значение скорости износа M_v=0,27;

-Стандартное отклонение скорости износа S_v=0,023.

Расчет ресурса оборудования по времени внезапного отказа. Для определения надежности оборудования необходимо провести статистические испытания. Моделирование таких испытаний производится с помощью генерации случайных чисел о наработке до отказа по следующим параметрам: N=292, Mt=51,73, St=9,51. Первые 10 чисел набора данных по наработке до внезапного отказа представлены в таблице 1.

Таблица 1 – Первые 10 чисел набора случайных данных о наработке до внезапного отказа

48,87

39,58

54,05

63,87

63,13

68,21

30,96

49,50

62,14

41,40

Определение вероятности безотказной работы оборудования. Для определения вероятности безотказной работы оборудования определим

распределение частот по наработке. Полученную таблицу частот дополним двумя столбцами - «Сумма» и «ВБР». В столбце «Сумма» рассчитывается сумма частот нарастающим итогом. Вероятность безотказной работы (ВБР) определена по формуле ВБР = 1 – Сумма/N, где N - сумма частот по всем карманам (табл. 2).

Таблица 2 - Расчет вероятности безотказной работы

Карман	Частота	Сумма	ВБР
25,39255193			0,996575
28,52795175			0,989726
31,66335158			0,976027
34,7987514			0,969178
37,93415123			0,928082
41,06955105			0,890411
44,20495088			0,784247
47,3403507			0,691781
50,47575052			0,589041
53,61115035			0,455479
56,74655017			0,342466
59,88195			0,236301
63,01734982			0,160959
66,15274965			0,078767
69,28814947			0,041096
72,4235493			0,017123
75,55894912			0,003425
Еще

Построим график зависимости вероятности безотказной работы от наработки (рис. 1).

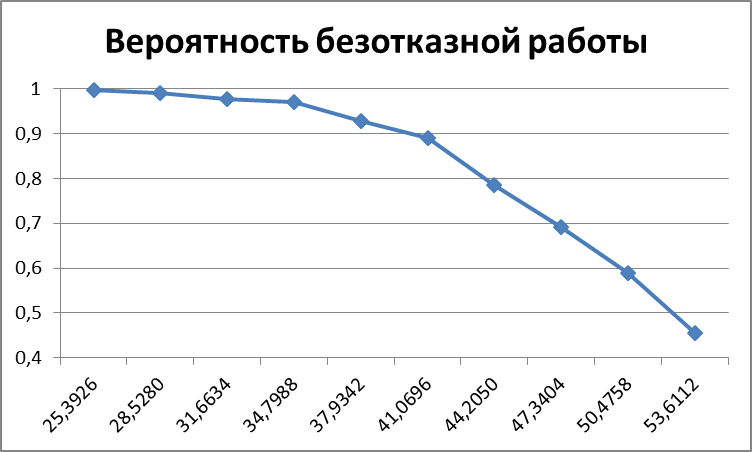
Рис. 1 Вероятность безотказной работы оборудования

Расчет наработки по нормативу. Выберем два значения вероятности и наработки, по которым определим

нормативный срок проведения ремонта оборудования. Одно значение (Р1) должно быть больше Рн, а другое (Р2) - меньше Рн. Из таблицы 2 выберем значения наработки Р1 и Р2 для выбранных точек.

№	P	T
	0,928	37,93
	0,89	41,2

По формуле интерполяции:

Tн = Т1 + (Р1-Рн)*(Т2-Т1)/(Р1-Р2)

получим значение наработки, соответствующее Рн = 0,9:

Tн = 37,93 +(0,928 – 0,9)*( 41,2 – 37,93)/( 0,928 - 0,89) = 40,34

Расчет времени работы до нормативного ремонта оборудования. Число оборудования, находящегося в эксплуатации, Nоб = 20 единиц оборудования. Это оборудование было установлено в разные сроки. Срок начала работы оборудования Т(нач) определяется с помощью генерации чисел с равномерным распределением от 1 до 10.

Время начала планового периода Тп = 20. Таким образом, к началу

планового периода каждое оборудование проработало разные сроки. Время работы оборудования определяется по формуле:

Т(раб) = Тп – Т(нач)

Тогда время до проведения ремонта по нормативу Т(норм ) для каждой единицы оборудования определяется по формуле:

Т(норм) = Тн – Т(раб)

Расчет времени проведения ремонта оборудования по нормативу проводится в таблице 3.

Таблица 3 – Расчет времени до проведения ремонта по нормативу

№	Т(нач)	Т(pаб)	Т(ноpм)
	1,31	18,69	21,65
	6,10	13,90	26,44
	7,62	12,38	27,96
	9,38	10,62	29,72
	7,74	12,26	28,08
	1,56	18,44	21,90
	4,52	15,48	24,86
	4,58	15,42	24,92
	5,42	14,58	25,76
	1,77	18,23	22,11
	5,66	14,34	26,00
	6,05	13,95	26,39
	9,67	10,33	30,01
	9,93	10,07	30,27
	2,70	17,30	23,04
	3,57	16,43	23,91
	8,46	11,54	28,80
	5,79	14,21	26,13
	4,87	15,13	25,21
	2,63	17,37	22,97

В результате ранжирования оборудования по времени проведения ремонта по нормативу получим (табл. 4).

Таблица 4 – Список очередности ремонта оборудования

№	Т(ноpм)
	21,65
	21,9
	22,11
	22,97
	23,04
	23,91
	24,86
	24,92
	25,21
	25,76

	26,13
	26,39
	26,44
	27,96
	28,08
	28,8
	29,72
	30,01
	30,27

Из полученных данных видно, что группа оборудования: 1,6, 10, 20,15 имеет наименьший ресурс (время до проведения ремонта по нормативу) и по этому критерию должна быть отремонтирована в первую очередь.

Расчет ресурса оборудования по времени наступления постепенного отказа.

Параметрическая модель износа. Линейная модель износа параметра Х имеет следующий вид:

Х = V*t, где V – случайная функция скорости износа.

На основе параметров Mv = 0,27 и Sv = 0,023 сгенерируем скорость износа для 20 единиц оборудования.

Данные скорости износа приведены в столбце V таблицы 5. На основе полученных данных произведем расчет времени работы каждой единицы оборудования до отказа по формуле:

Т(отк) = Хдоп/V, где Хдоп = 10 - заданное допустимое значение износа.

Используя данные таблицы 3 по наработке к началу планового периода Т(раб) и расчетные данные о времени возникновения постепенного отказа Т(отк), рассчитаем время возникновения постепенного отказа по формуле:

Т(пар) = Т(отк) – Т(раб)

Расчет выполнен в таблице 5.

Таблица 5 – Расчет времени работы оборудования до параметрического отказа

№	V	Т(отк)	Т(pаб)	Т(пар)
	0,276	36,260	18,69	17,573
	0,262	38,117	13,90	24,221
	0,251	39,776	12,38	27,396
	0,255	39,271	10,62	28,651
	0,299	33,490	12,26	21,226
	0,289	34,569	18,44	16,129
	0,281	35,562	15,48	20,078
	0,266	37,580	15,42	22,161
	0,288	34,669	14,58	20,092
	0,315	31,743	18,23	13,512
	0,232	43,094	14,34	28,752
	0,254	39,427	13,95	25,482
	0,335	29,849	10,33	19,521
	0,273	36,641	10,07	26,574
	0,269	37,233	17,30	19,936
	0,252	39,604	16,43	23,170
	0,239	41,761	11,54	30,221
	0,276	36,220	14,21	22,011
	0,293	34,119	15,13	18,987
	0,301	33,187	17,37	15,814

В результате ранжирования оборудования по времени наступления постепенного отказа получим (табл. 6).

Таблица 6 – Список очередности ремонта оборудования

№	Т(отк)
	13,512
	15,814
	16,129
	17,573
	18,987
	19,521
	19,936
	20,078
	20,092
	21,226
	22,011
	22,161
	23,17
	24,221
	25,482
	26,574
	27,396
	28,651
	28,752
	30,221

Из полученных данных видно, что группа оборудования: 10,20, 6, 1, 19 –имеет наименьший ресурс (время до возникновения постепенного отказа) и по этому критерию должна быть отремонтирована в первую очередь.

Сравнивая ранжированные списки оборудования по двум критериям назначения ремонтов определяем, что в первые 5 единиц оборудования, имеющих приоритет в назначении ремонта, попали следующие единицы оборудования: 1,6, 10, 20,15.

12 Следующая ⇒