
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задание.. Задание.. Задание.. группа. Используя геометрическую модель – числовую окружность на координатной плоскости, решим уравнение . Отметим на окружности точки М и Р с абсциссой 0,5 (она лежит на прямой х. = 0,5). Точка М соответствует числу , а знач
Тема: «Простейшие тригонометрические уравнения.»
а) Вычислить:
 , т.к.
, т.к. 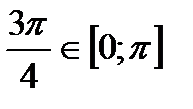
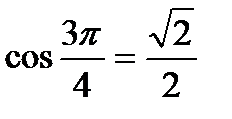 ,
,
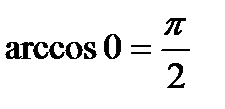 , т.к.
, т.к.  ,
, 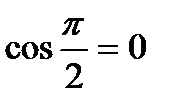 .
.
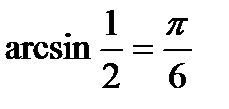 , т.к.
, т.к. 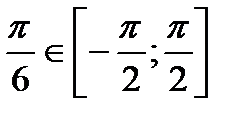 ,
, 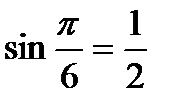 ,
,
 , т.к.
, т.к. 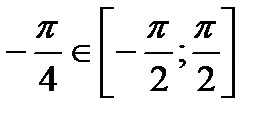 ,
, 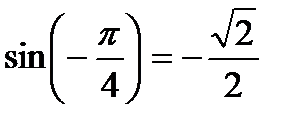 ,
,
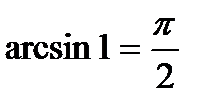 , т.к.
, т.к. 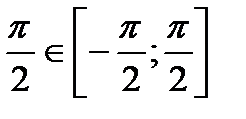 ,
, 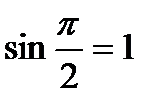 .
.
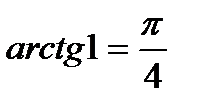 , т.к.
, т.к.  ,
, 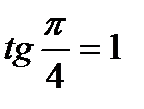 ;
;
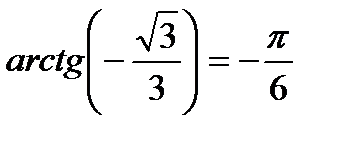 , т.к.
, т.к. 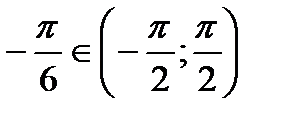 ,
, 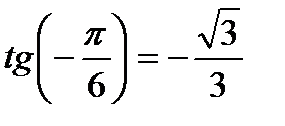 ,
,
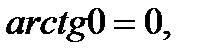 т.к.
т.к. 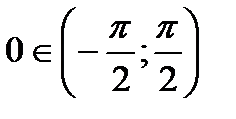
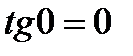 .
.
1) arcsin  ;
;
2) arсcos 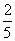 ;
;
3) arсcos 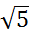 ;
;
4) arcsin 1,5 ;
5) arctg 5;
6) arcсtg 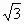 ;
;
7) arccos 1,8 ;
8) arcsin π.
Тригонометрическими уравненияминазывают уравнения, в которых переменная содержится под знаком тригонометрических функций.
Для решения различных видов тригонометрических уравнений необходимо уметь решать простейшие тригонометрические уравнения. К ним относятся уравнения вида: 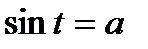 ,
, 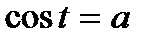 ,
, 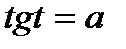 ,
, 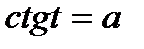 . Некоторые представления о решении таких уравнений мы уже имеем. Задача нашего урока состоит в следующем: нам необходимо вывести общие формулы для решения простейших тригонометрических уравнений.
. Некоторые представления о решении таких уравнений мы уже имеем. Задача нашего урока состоит в следующем: нам необходимо вывести общие формулы для решения простейших тригонометрических уравнений.
Задание.
1. Используя геометрическую модель – числовую окружность на координатной плоскости, решите уравнение:
а) 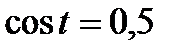 ; б)
; б) 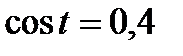 ; в)
; в) 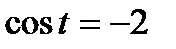 .
.
2. Для каждого значения параметра a, решите уравнение  .
.
Задание.
1. Используя геометрическую модель – числовую окружность на координатной плоскости, решите уравнение:
а) 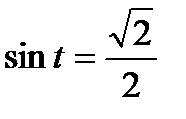 ; б)
; б) 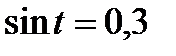 ; в)
; в) 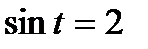 .
.
2. Для каждого значения параметра a, решите уравнение 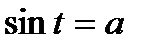 .
.
Задание.
1. Используя геометрическую модель – числовую окружность на координатной плоскости, решите уравнение:
а)  ; б)
; б) 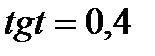 ; в)
; в) 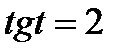 .
.
2. Для каждого значения параметра a, решите уравнение 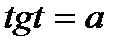 .
.
1 группа. Используя геометрическую модель – числовую окружность на координатной плоскости, решим уравнение . Отметим на окружности точки М и Р с абсциссой 0,5 (она лежит на прямой х. = 0,5). Точка М соответствует числу , а значит, всем числам вида . Точка Р соответствует числу , а, следовательно, и всем числам вида . В итоге получаем две серии решений уравнения: .
Используя геометрическую модель – числовую окружность на координатной плоскости, решим уравнение 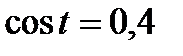 . Отметим на окружности точки М и Р с абсциссой 0,4 (она лежит на прямой х. = 0,4). Это уравнение имеет два решения, но каких мы не знаем. Наверно, необходима новая математическая формула.
. Отметим на окружности точки М и Р с абсциссой 0,4 (она лежит на прямой х. = 0,4). Это уравнение имеет два решения, но каких мы не знаем. Наверно, необходима новая математическая формула.
Используя геометрическую модель – числовую окружность на координатной плоскости, решим уравнение 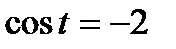 . Это уравнение не имеет решений, т.к. прямая х. = -2 не пересекает числовую окружность.
. Это уравнение не имеет решений, т.к. прямая х. = -2 не пересекает числовую окружность.
Вывод: уравнение  имеет две серии решений при
имеет две серии решений при 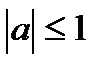 , не имеет решений при
, не имеет решений при 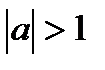 . Для решения уравнения
. Для решения уравнения  необходимо ввести новую математическую формулу.
необходимо ввести новую математическую формулу.
2 группа. Используя геометрическую модель – числовую окружность на координатной плоскости, решим уравнение 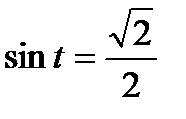 . Отметим на окружности точки М и Р с ординатой
. Отметим на окружности точки М и Р с ординатой 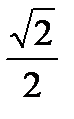 (она лежит на прямой
(она лежит на прямой 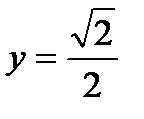 ). Точка М соответствует числу
). Точка М соответствует числу 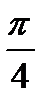 , а значит, всем числам вида
, а значит, всем числам вида
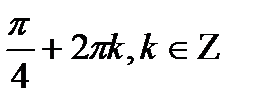 . Точка Р соответствует числу
. Точка Р соответствует числу  , а, следовательно, и всем числам вида
, а, следовательно, и всем числам вида
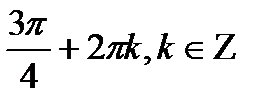 . В итоге получаем две серии решений уравнения:
. В итоге получаем две серии решений уравнения: 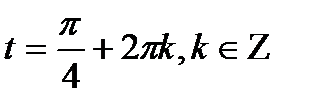 ;
; 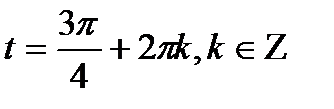 .
.
Используя геометрическую модель – числовую окружность на координатной плоскости, решим уравнение 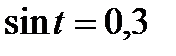 . Отметим на окружности точки М и Р с ординатой 0,3 (она лежит на прямой у = 0,3). Это уравнение имеет два решения, но каких мы не знаем.
. Отметим на окружности точки М и Р с ординатой 0,3 (она лежит на прямой у = 0,3). Это уравнение имеет два решения, но каких мы не знаем.
Используя геометрическую модель – числовую окружность на координатной плоскости, решим уравнение 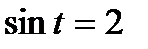 . Это уравнение не имеет решений, т.к. прямая у = 2 не пересекает числовую окружность.
. Это уравнение не имеет решений, т.к. прямая у = 2 не пересекает числовую окружность.
Вывод: уравнение 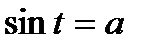 имеет две серии решений при
имеет две серии решений при 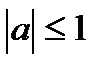 , не имеет решений при
, не имеет решений при 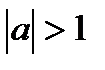 . Решение уравнения
. Решение уравнения 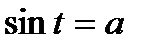 вызвало у нас затруднение.
вызвало у нас затруднение.
Мы считаем, что для решения уравнения 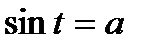 также необходимо ввести новую математическую формулу.
также необходимо ввести новую математическую формулу.
3 группа. Используя геометрическую модель – числовую окружность на координатной плоскости, решим уравнение  . На линии тангенсов отметим число
. На линии тангенсов отметим число 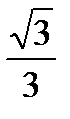 . Прямая ОТ пересекает окружность в двух точках М, Р. Точка М соответствует числу
. Прямая ОТ пересекает окружность в двух точках М, Р. Точка М соответствует числу 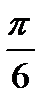 , точка Р соответствует числу -
, точка Р соответствует числу - 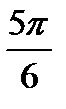 . Учитывая периодичность функции y = tgx, можно сказать, что уравнение
. Учитывая периодичность функции y = tgx, можно сказать, что уравнение  имеет одну серию решений
имеет одну серию решений 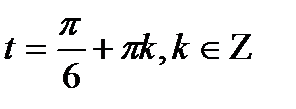 .
.
Используя геометрическую модель – числовую окружность на координатной плоскости, решим уравнение 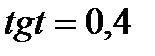 . На линии тангенсов отметим число 0,4. Прямая ОТ пересекает окружность в двух точках М, Р. Это уравнение имеет одну серию решений, но записать это решение мы не смогли .
. На линии тангенсов отметим число 0,4. Прямая ОТ пересекает окружность в двух точках М, Р. Это уравнение имеет одну серию решений, но записать это решение мы не смогли .
Используя геометрическую модель – числовую окружность на координатной плоскости, решим уравнение 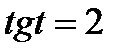 . На линии тангенсов отметим число 2. Прямая ОТ пересекает окружность в двух точках М, Р. Это уравнение имеет одну серию решений, но записать это решение мы не смогли . Наверно, здесь имеют место математические термины, которые мы изучили на прошлом уроке-это arctgа
. На линии тангенсов отметим число 2. Прямая ОТ пересекает окружность в двух точках М, Р. Это уравнение имеет одну серию решений, но записать это решение мы не смогли . Наверно, здесь имеют место математические термины, которые мы изучили на прошлом уроке-это arctgа
Вывод: уравнение 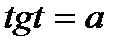 имеет одну серию решений при любом значении параметра а. Для решения уравнения
имеет одну серию решений при любом значении параметра а. Для решения уравнения 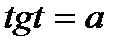 необходимо ввести новую формулу.
необходимо ввести новую формулу.
Если 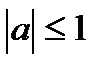 , то уравнение
, то уравнение  имеет решения
имеет решения 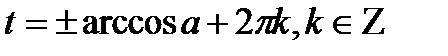 .
.
Если а = -1; 0; 1, то пользуются более простыми формулами:
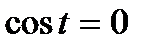 ,
, 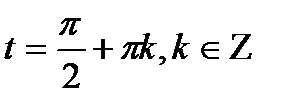 ;
; 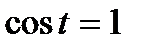 ,
,  ;
; 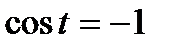 ,
, 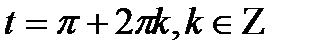 .
.
Если 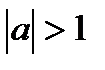 , то уравнение
, то уравнение  решений не имеет.
решений не имеет.
Если 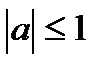 , то уравнение
, то уравнение 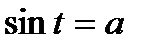 имеет две серии решений
имеет две серии решений 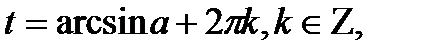
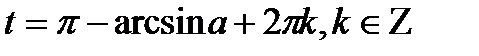 . Эти две формулы можно объединить одной формулой. Перепишем эти формулы следующим образом:
. Эти две формулы можно объединить одной формулой. Перепишем эти формулы следующим образом: 
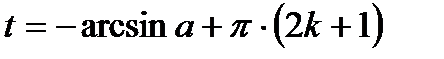 . Замечаем, что если перед arcsin a стоит знак «плюс», то у числа
. Замечаем, что если перед arcsin a стоит знак «плюс», то у числа 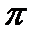 множителем является четное число 2k. Если же перед arcsin a стоит знак «минус», то у числа
множителем является четное число 2k. Если же перед arcsin a стоит знак «минус», то у числа 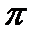 множителем является нечетное число 2k + 1. Это наблюдение позволяет записать общую формулу для решения уравнения
множителем является нечетное число 2k + 1. Это наблюдение позволяет записать общую формулу для решения уравнения 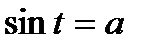 :
: 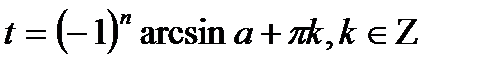 .
.
Если а = -1; 0; 1, то пользуются более простыми формулами:
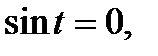
 ;
; 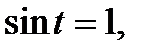
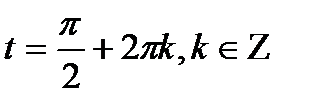 ;
; 
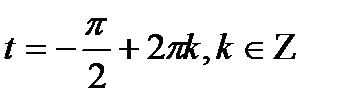 .
.
Если 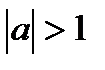 , то уравнение
, то уравнение 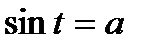 решений не имеет.
решений не имеет.
Уравнение 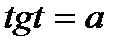 имеет решения
имеет решения 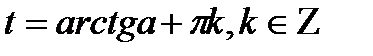 для любого значения а.
для любого значения а.
1)Учащиеся, пользуясь полученными формулами, решают уравнения.
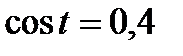 ,
, 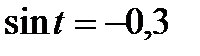 ,
, 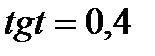 ,
, 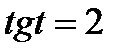 .
.
Решите уравнения: У доски 2 учащихся по очереди решают уравнения: слайд 17
2) 2sin х = 1, 2cosх = 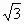 ;
;
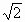 cosх –1 =0,
cosх –1 =0, 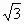 tgх – 1 = 0; ctgх = 2,5
tgх – 1 = 0; ctgх = 2,5
VI.Самостоятельная работа.
1) sinх= - 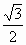 ,
,
2) cosх = 1,1,
3 ) 2sinх – 1 = 0,
4) tgх =1,7.
5) cosх = 0
6) sinх = 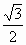
7) 2 cosх - 2=0,
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|