
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Рациональные, иррациональные, показательные и тригонометрические неравенства
Тема: Рациональные, иррациональные, показательные и тригонометрические неравенства
Понятие показательного неравенства.
При решении неравенств вида 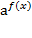
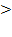
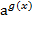 следует помнить, что показательная функция y = аx возрастает при а
следует помнить, что показательная функция y = аx возрастает при а 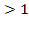 и убывает при 0
и убывает при 0 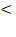 а
а 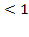 . Значит, в случае, когда а
. Значит, в случае, когда а 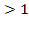 , от неравенства
, от неравенства 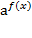
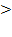
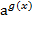 следует переходить к неравенству
следует переходить к неравенству 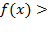
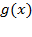 . В случае же, когда 0
. В случае же, когда 0 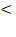 а
а 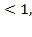 от неравенства
от неравенства 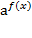
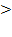
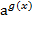 следует переходить к неравенству
следует переходить к неравенству 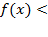
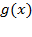 .
.
Понятие тригонометрических неравенств.
Определение.
Простейшими тригонометрическими неравенствами называют неравенства вида:
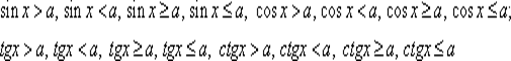
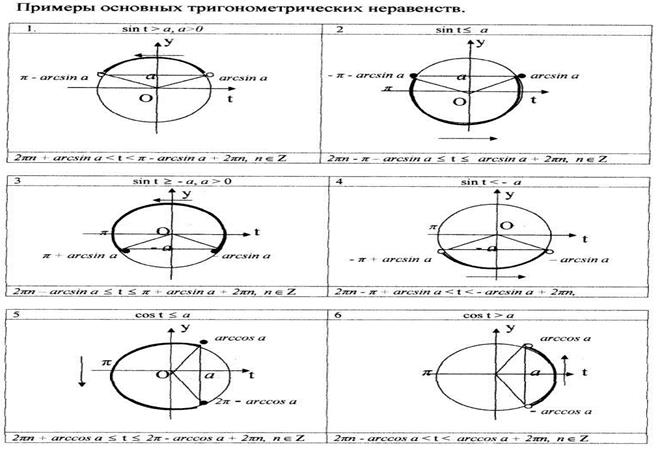
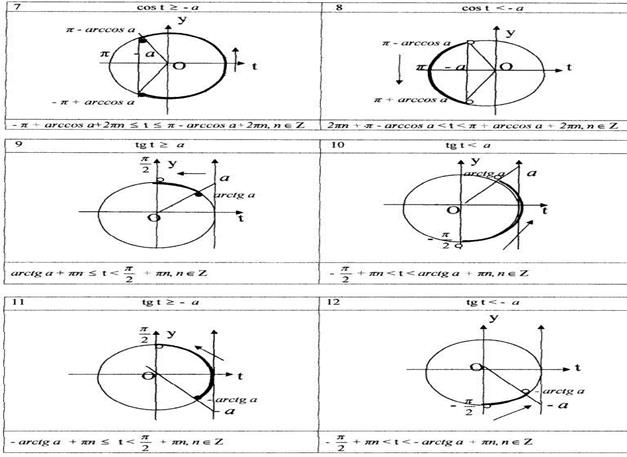
Алгоритм решения тригонометрических неравенств с помощью единичной окружности:
1. На оси, соответствующей заданной тригонометрической функции, отметить данное числовое значение этой функции.
2. Провести через отмеченную точку прямую, пересекающую единичную окружность.
3. Выделить точки пересечения прямой и окружности с учетом строгого или нестрогого знака неравенства.
4. Выделить дугу окружности, на которой расположены решения неравенства.
5. Определить значения углов в начальной и конечной точках дуги окружности.
6. Записать решение неравенства с учетом периодичности заданной тригонометрической функции.
3. Закрепление
Решение показательные неравенств:1) 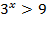 ; 2)
; 2) 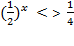 ; 3)
; 3) 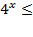
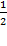 ;
;
4) 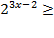
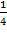 ; 5)
; 5) 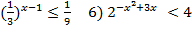
 16; 2)
16; 2)  ; 3)
; 3) 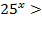
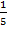 ; 4)
; 4) 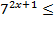
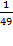 ;
;
5) 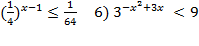
Решите тригонометрические неравенство:
1. sin 3x 
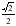
2. tg x  - 1
- 1
3. cos 2x  -
- 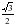
4. cos (x + 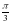 )
)
1. sin x  -
- 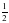
2. cos (3x - 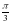 )
)
3. cos 2x 
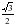
4. tg x  -
- 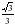
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|