
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: «Применение интеграла к вычислению физических величин и площадей.
Тема: «Применение интеграла к вычислению физических величин и площадей.
· Найти первообразные для функций:
а) f(x) =х7
б) f(x) = 7х6
в) f(x) =sin(2x)
- На каком рисунке изображена фигура, не являющаяся криволинейной трапецией?
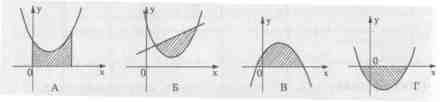
- С помощью формулы Ньютона-Лейбница вычисляют
А)первообразную Б) площадь криволинейной трапеции в) интеграл г) производную
А если фигура не является криволинейной трапецией, как найти ее площадь? Я думаю, что вы догадались, чему будет посвящен сегодняшний урок. Запишите тему урока: «Вычисление площадей плоских фигур с помощью определенного интеграла».
Мотивация. Используется проблемный метод(7 мин)
На предыдущих занятиях мы вычисляли площади криволинейных трапеций.
Какая фигура называется криволинейной трапецией?
Сегодня мы продолжим решать задачи на нахождение площадей различных фигур с помощью интегралов.
- Как вычислить площадь фигуры, ограниченной линиями: y = f (x); y = 0; x = a; x = b.(криволинейная трапеция)
a b |
Выполнить записи в тетрадях.
Как вычислить площадь фигуры, ограниченной линиями:y = f (x); y = 0; x = a; x = b
 a b
a b
| 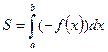
|
- Как вычислить площадь фигуры, ограниченной линиями: y = f (x); y = g (x); y = 0.
| 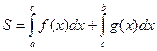
| |||||||||||||||||||||||||||
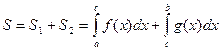
- Как вычислить площадь фигуры, ограниченной линиями: y = f (x); y = g (x)
y=g(x)
|
.
Аналогично, при рассмотрении второй фигуры, студенты приходят к выводу о том, что площадь данной фигуры можно найти как разность площадей двух криволинейных трапеций, опирающихся на один отрезок.
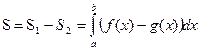
1.Вычислить площадь фигуры, ограниченной графиками функций у = 4 – х2 и у = х + 2
2.Вычислить площадь фигуры, ограниченной графиками функций у = 4 – х2 и у = х + 2 и осью ох.
Перед выполнением работы, преподаватель вместе со студентами составляет алгоритм нахождения площади фигур.
б) Самостоятельная работа
Алгоритм выполнения задания.
1.В прямоугольной системе координат изобразите графики соответствующих функций.
2.Заштрихуйте фигуру, площадь которой нужно найти.
3.Запишите формулу для вычисления площади данной фигуры в общем виде.
4.Запишите данную формулу с использованием данных функций.
5.Определите пределы интегрирования
6.Вычислите площадь.
Интегральное исчисление дает богатый математический аппарат для моделирования и исследования процессов, происходящих в экономике. Интегральное исчисление в экономике используют для прогнозирования материальных затрат, нахождения потребительского излишка (разница между той денежной суммой, за которую производитель был бы готов продать 100 единиц товара, и той суммой, которую он реально получает при продаже этого количества товара), определения объема выпуска продукции, определения экономической эффективности капитальных вложений (задача дисконтирования). И это далеко не полный список приложений интегрального исчисления в экономике.
Вспомним несколько экономических понятий и обозначений.
Как в экономике определяется спрос?
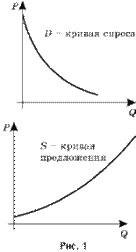
(Спрос на данный товар(D–demand) графически изображается в виде кривой с отрицательным наклоном, отражающей взаимосвязь между ценой P (price) единицы этого товара и количеством товара Q (quantity), которое потребители готовы купить при каждой заданной цене.)
Что обозначает отрицательный наклон кривой?
(Отрицательный наклон кривой спроса имеет очевидное объяснение: чем дороже товар, тем меньше количество товара, которое покупатели готовы купить, и наоборот.)
Другое ключевое понятие экономической теории – предложение (S–supply) товара изображается графически в виде кривой с положительным наклоном, отражающей взаимосвязь между ценой единицы этого товара P и количеством товара Q, которое потребители готовы продать при каждой цене.
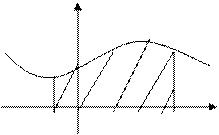
И, наконец, вспомним еще одно понятие, играющее большую роль в моделировании экономических процессов – рыночное равновесие (equilibrium). Состояние равновесия характеризуют такие цена и количество, при которых объем спроса совпадает с величиной предложения, а графически рыночное равновесие изображается точкой пересечения кривых спроса и предложения (рис. 2), E*(p*; q*) – точка равновесия.
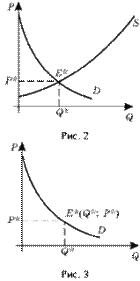
Перейдем теперь к рассмотрению приложений интегрального анализа для определения потребительского излишка.
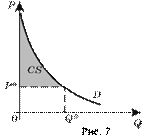
Фигура В является криволинейной трапецией? (Да)
Как можно вычислить площадь этой фигуры с помощью интеграла?
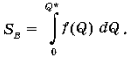
Разберемся с частями фигуры В с точки зрения экономики.
Какой денежной сумме соответствует площадь фигуры B?
(Площадь фигуры B соответствует общей денежной сумме, которую потребитель готов потратить на покупку Q* единиц товара)
Какой денежной сумме соответствует площадь прямоугольника?
(Площадь прямоугольника – реальные расходы на приобретение.)
Как вычислить площадь этого прямоугольника?(Q*∙p*)
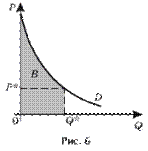
Какая часть фигуры отвечает за излишек потребителя? (СS)
Используя формулу для вычисления площадей криволинейной трапеции , потребительский излишек можно посчитать по следующей формуле
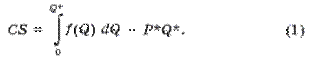
Далее рассмотрим задачу на определение излишка потребителя.
Задача. Известно, что спрос на некоторый товар описывается функцией 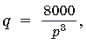 а предложение данного товара характеризуется функцией q = 500p. Найдите величину излишка потребителя при покупке данного товара.
а предложение данного товара характеризуется функцией q = 500p. Найдите величину излишка потребителя при покупке данного товара.
Решение. Для расчета излишка потребителя сначала определим параметры рыночного равновесия (p*; q*). Для этого решим систему уравнений
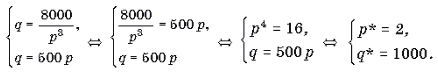 Таким образом, p* = 2, q* = 1000.
Таким образом, p* = 2, q* = 1000.
Запишем формулу для вычисления потребительского излишка (1), где f(q) – функция, обратная функции 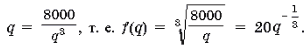
Отсюда 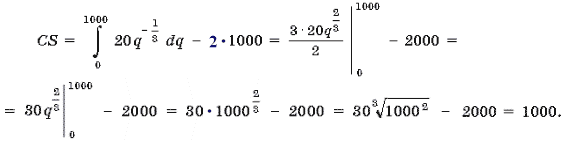
5.Домашнее заданиеЗадача 1 Фигура ограничена линиями у = 2- х2, у = х. Заштрихуйте данную фигуру и вычислите ее площадь.
Задача 2. Известно, что спрос на некоторый товар задается функцией p = 4 – q2, где q – количество товара (в шт.), p – цена единицы товара (в руб.), а равновесие на рынке данного товара достигается при p* = q* = 1. Определите величину потребительского излишка.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
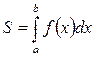

 y=f(x)
y=f(x)