Контакты

Случайная статья

Выполнение работы. Упражнение 1. Упражнение 2

⇐ ПредыдущаяСтр 2 из 2

(2)

Решив систему уравнений (2)относительно Т и I исходим:

(3) (4)

Для дальнейшего преобразования выражений (3) и (4) используем соотношение:

(5)

Оно связывает линейное и угловое ускорения точек, лежащих на оси маятника, и тот факт, что движение маятника равноускоренно и, следовательно:

(6)

h - длина маятника, t- время его падения.

С учётом (5) и (6), для силы натяжения нити и момента инерции маятника окончательно имеем:

(7) (8)

d - внешний диаметр оси маятника.

Выполнение работы

Упражнение 1

Определение ускорения движения маятника и силы натяжения в нитях подвеса.

1) На ролик маятника наложили кольцо, прижимая его до упора.

2) На ось маятника равномерно, виток к витку, намотали нить подвеса, и зафиксировали её.

3) Определили время падения маятника:

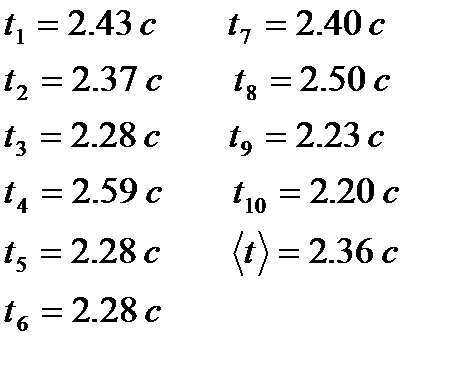
4) Определили длину маятника:

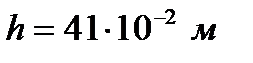
5) Вычислили значение ускорения маятника:

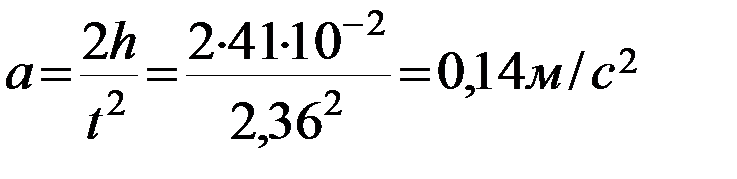
6) Определили массу маятника:

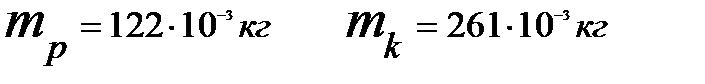
где 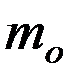- масса оси маятника, 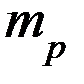- масса ролика, 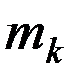- масса кольца.

7) Рассчитали силу натяжения нитей:

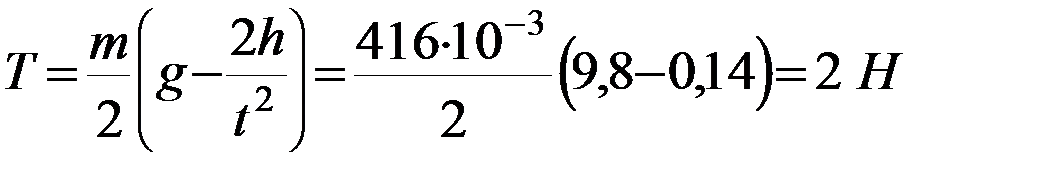
Упражнение 2

Определение момента инерции маятника.

1) Определили экспериментальное значение момента инерции 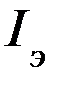данного маятника:

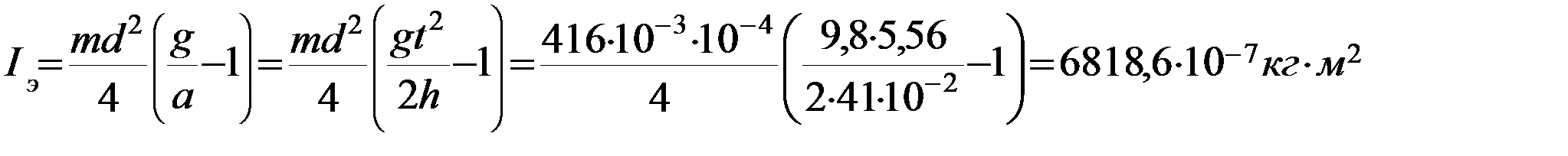
2) Измерили диаметры оси маятника, ролика и съёмного кольца:

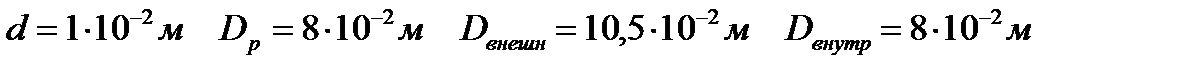
3) Вычислили теоретическое значение 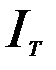момента инерции маятника Максвелла по формуле:

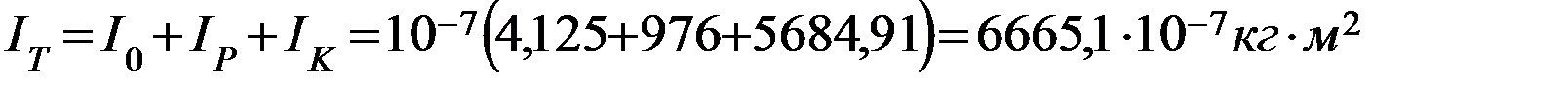
где 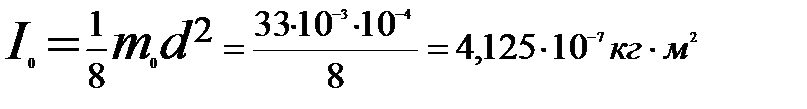- момент инерции оси маятника.

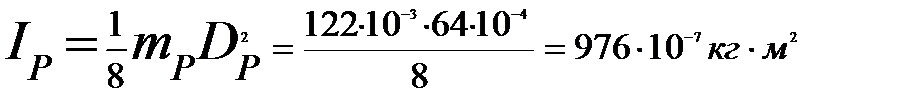- момент инерции ролика.

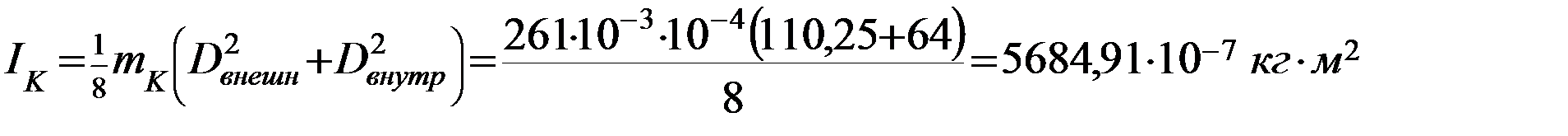- момент инерции кольца.

4) Сравнили значения Iэ и IТ:

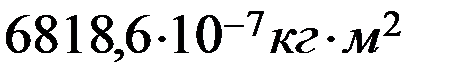
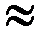
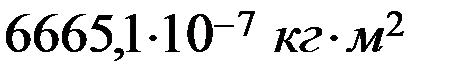
Iэ 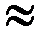IТ

Вывод:определили ускорение движения маятника Максвелла и силы натяжения в нитях подвеса. Определили момент инерции маятника Максвелла теоретически и экспериментально, выяснили, что значения моментов инерции приблизительно равны.

⇐ Предыдущая 12

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.