
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Поверхности второго порядка: сфера, эллипсоид, конус, гиперболоид, параболоид.
21. Поверхности второго порядка: сфера, эллипсоид, конус, гиперболоид, параболоид.
Сфера— замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, называемой центром сферы. Сфера также является телом вращения, образованным при вращении полуокружности вокруг своего диаметра.
Сфера является частным случаем эллипсоида, у которого все три оси (полуоси, радиусы) равны.
S = 4πr2
S = πd2
Конус.
Поверхность, образованная прямыми линиями, проходящими через данную точку Р и
пересекающими данную плоскую линию L (не проходящую через Р) называется
конической поверхностью или конусом. При этом линия L называется
направляющей конуса, точка Р – ее вершиной, а прямая, описывающая
поверхность, называется образующей.
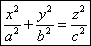 - уравнение конуса
- уравнение конуса
Эллипсоид.
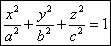
Рассмотрим сечение поверхности с плоскостями, параллельными xOy. Уравнения
таких плоскостей z=h, где h – любое число. Линия, получаемая в сечении,
определяется двумя уравнениями:
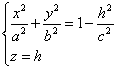
Если |h|>c, c>0, то 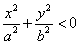 точек пересечения поверхности с плоскостями z=h нет.
точек пересечения поверхности с плоскостями z=h нет.
Если |h|=c, т.е. h=±c, то 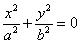
. Линия пересечения вырождается в две точки (0;0;с) и (0;0;-с). Плоскости z=c и
z=–c касаются поверхности.
Если |h|<c, то уравнения можно переписать в виде: 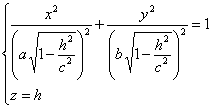
Линия пересечения есть эллипс с полуосями.
Эллипсоид – замкнутая овальная поверхность, где a,b,с – полуоси. Если все
они различны, то эллипсоид называется трехосным. Если какие-либо две
полуоси равны, то тело называется эллипсоид вращения, если a=b=c, то тело
называется сферой x2+y2+z2=R2
Гиперболоид— это вид поверхности второго порядка в трёхмерном пространстве, задаваемый в декартовых координатах уравнением
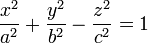 (однополостный гиперболоид),
(однополостный гиперболоид),
где a и b — действительные полуоси, а c — мнимая полуось;
или 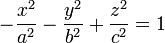 (двуполостный гиперболоид),
(двуполостный гиперболоид),
где a и b — мнимые полуоси, а c — действительная полуось.
При этом a, b и c — положительные числа.
Если a = b, то такая поверхность называется гиперболоидом вращения. Однополостный гиперболоид вращения может быть получен вращением гиперболы вокруг её мнимой оси, двуполостный — вокруг действительной. Двуполостный гиперболоид вращения также является геометрическим местом точек P, модуль разности расстояний от которых до двух заданных точек A и B постоянен: | AP − BP | = const. В этом случае A и B называются фокусами гиперболоида.
Однополостный гиперболоид является дважды линейчатой поверхностью; если он является гиперболоидом вращения, то он может быть получен вращением прямой вокруг другой прямой, скрещивающейся с ней
Параболоиды.
Эллиптический. При пересечении поверхности координатами плоскостями Oxz и Oyz получается соответственно параболы 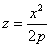 и
и 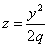 .
.
Таким образом, поверхность, определяемая уравнением, имеет вид выпуклой, бесконечно
расширяющейся чаши.
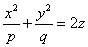
Гиперболический.
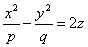
Рассечем поверхность плоскостями z=h. Получим кривую
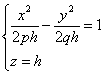 которая при всех h≠0 является гиперболой. При h>0 ее действительные оси параллельны оси Ox, при h<0 – параллельные оси Oy. При h=0 линия
которая при всех h≠0 является гиперболой. При h>0 ее действительные оси параллельны оси Ox, при h<0 – параллельные оси Oy. При h=0 линия
пересечения распадается на пару пересекающихся прямых:
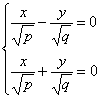
При пересечении поверхности плоскостями, параллельности плоскости Oxz (y=h),
будут получаться параболы, ветви которых направлены вверх.
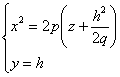
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|