
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Занятие №112
Специальность 21.02.04 Землеустройство.
Первый курс, 15 группа, 16 группа.
Неделя с 8.06 по 13.06.2020
Занятие №112
Тема: Неравенства. Основные приемы их решения.
План:
1.Неравенства.
2.Виды неравенств.
3.Основные приемы их решения.
1. Неравенство это два числовых или буквенных выражения, соединенных знаками >, <, ≥, ≤ или ≠. Решить неравенство означает найти такие значения переменной x, при которых данное неравенство становится верным. Значение переменной, при котором неравенство становится верным, называется решением неравенства.
Неравенства, содержащие знаки >, < называют строгими. А неравенства, содержащие знаки ≥, ≤ называют нестрогими. Равносильными называют неравенства, решения которых совпадают.
Процесс решения неравенств во многом схож с процессом решения уравнений. При решении неравенств применяются свойства:
1. Если к левой и правой части неравенства прибавить или вычесть одно и то же число, то знак неравенства не изменится.
2. Если обе части неравенства умножить или разделить на одно и то же положительное число, то знак неравенства не изменится.
3. Если обе части неравенства умножить или разделить на одно и то же отрицательное число, то знак неравенства изменится на противоположный.
2. Рассмотрим основные виды неравенств:
1) Линейные неравенства с одной переменной – это неравенства вида ах>b, ах<b, ах≥b, ах≤ b . Рассмотрим решение примеров.
Пример1. Решить неравенство 15x-23(x+1)>2x+11.
Решение рассмотрим подробно. Раскроем скобки в левой части неравенства: 15x-23x-23>2x+11.
Перенесём с противоположными знаками слагаемые и приведём подобные: 15x-23x-2x>11+23, -10x>34.
Разделим обе части на -10 и изменим знак неравенства на противоположный: x<-3,4. Множество решений представляет собой промежуток (-∞;-3,4).
ОТВЕТ: (-∞;-3,4).
Пример 2. Решить неравенство.
2(х – 3)+5(1 – х)≥3(2х – 5).
Решение. Раскроем скобки:
2х – 6 +5 – 5х≥6х – 15,
- 3х - 1≥6х – 15.
- 3х – 6х≥ - 15+1,
- 9х≥ - 14.
Разделим обе части неравенства на отрицательное число – 9 и изменим знак неравенства: х≤14/9.
ОТВЕТ: (- ∞; 14/9].
Пример 3. Решить неравенство.
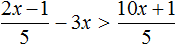
Решение:
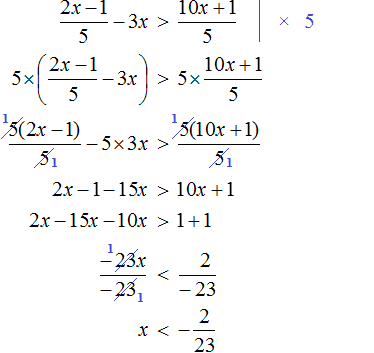

Ответ: 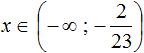
2) Квадратные неравенства – это неравенства вида ax²+bx+c>0 и ax²+bx+c<0. Для решения неравенств данного вида поступают следующим образом:
- находят дискриминант квадратного трёхчлена и выясняют, имеет ли трёхчлен корни;
- если трёхчлен имеет корни, то отмечают их на оси ОХ и через отмеченные точки проводят схематически параболу, ветви которой направлены вверх при a>0 или вниз при a<0; если трёхчлен не имеет корней, то схематически изображают параболу, расположенную в верхней полуплоскости при a>0 или в нижней при a<0;
- находят на оси ОХ промежутки, для которых точки параболы расположены выше оси ОХ (если решают неравенство ax²+bx+c>0) или ниже оси ОХ (если решают неравенство ax²+bx+c<0).
Пример 4.
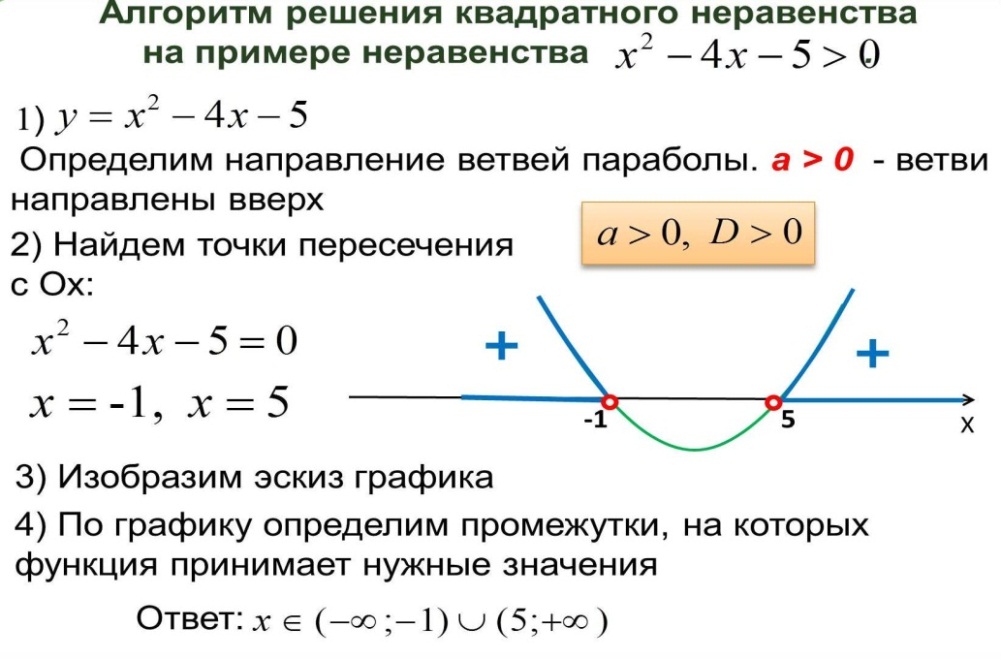
Пример 4.

При решении квадратных неравенств можно пользоваться следующей таблицей:

3) Рациональные неравенства - это дробные неравенства, в знаменателе которых стоит переменная. Основной метод решения – метод интервалов.
Алгоритм решения:

Пример 5. Решить неравенства:
1.
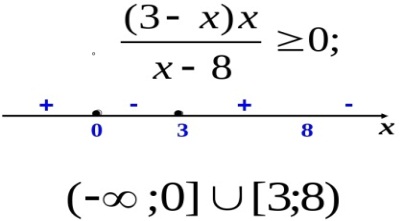 Ответ:
Ответ: 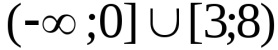
2.


При разложении числителя использовалась формула:
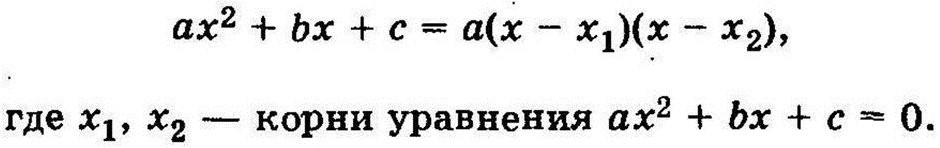
4) Иррациональные неравенства - неравенства, содержащие переменную под знаком радикала (корня). При решении иррациональных неравенств удобно пользоваться следующей таблицей.
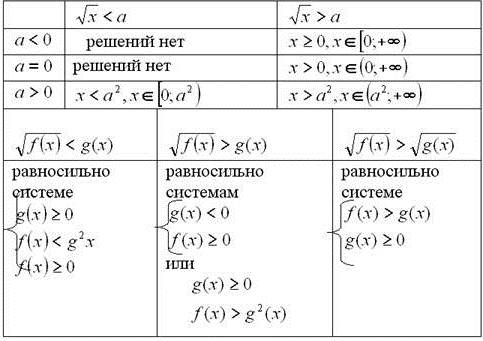
Примеры решения иррациональных неравенств.

Литература: Дадаян А.А. Математика: учебник— 3-е изд., испр. и доп. — М.: ИНФРА-М, 2019. — 544 с. — (Cреднее профессиональное образование). - Режим доступа: http://znanium.com/catalog/product/1006658, §4.4, с.88.
https://www.yaklass.ru/p/ege/matematika/podgotovka
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|